MinistepToTwostep • RsienaTwoStep

1. Getting started

rm(list=ls())

1.1. Basic functions

fsave <- function(x, file, location = "./data/processed/", ...) {
    if (!dir.exists(location))
        dir.create(location)
    datename <- substr(gsub("[:-]", "", Sys.time()), 1, 8)
    totalname <- paste(location, datename, file, sep = "")
    print(paste("SAVED: ", totalname, sep = ""))
    save(x, file = totalname)
}

fpackage.check <- function(packages) {
    lapply(packages, FUN = function(x) {
        if (!require(x, character.only = TRUE)) {
            install.packages(x, dependencies = TRUE)
            library(x, character.only = TRUE)
        }
    })
}

colorize <- function(x, color) {
    sprintf("<span style='color: %s;'>%s</span>", color, x)
}

1.2. Packages

packages = c("RsienaTwoStep", "doParallel", "ggplot2")

fpackage.check(packages)
#> Loading required package: RsienaTwoStep
#> Loading required package: foreach
#> Loading required package: doParallel
#> Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
#> logical.return = TRUE, : there is no package called 'doParallel'
#> Installing package into '/home/runner/work/_temp/Library'
#> (as 'lib' is unspecified)
#> also installing the dependencies 'listenv', 'parallelly', 'future', 'globals', 'shape', 'future.apply', 'numDeriv', 'progressr', 'SQUAREM', 'diagram', 'lava', 'tzdb', 'cpp11', 'prodlim', 'timechange', 'proxy', 'Rcpp', 'data.table', 'clock', 'gower', 'hardhat', 'ipred', 'lubridate', 'timeDate', 'e1071', 'ModelMetrics', 'plyr', 'pROC', 'recipes', 'reshape2', 'caret', 'mlbench', 'RUnit'
#> Loading required package: iterators
#> Loading required package: parallel
#> Loading required package: ggplot2
#> [[1]]
#> NULL
#> 
#> [[2]]
#>  [1] "doParallel"    "parallel"      "iterators"     "RsienaTwoStep"
#>  [5] "foreach"       "stats"         "graphics"      "grDevices"    
#>  [9] "utils"         "datasets"      "methods"       "base"         
#> 
#> [[3]]
#> NULL

2. Setting up cluster

no_cores <- detectCores() - 1
mycl <- makeCluster(rep("localhost", no_cores))
clusterEvalQ(mycl, library(RsienaTwoStep)) 
registerDoParallel(mycl)
#stopCluster(mycl)

3. Running simulations on toy data

3.1. Model 1: Degree and reciprocity

Let us assume people really don’t like to have a non-reciprocal tie but do like reciprocal ties a lot. (I only want to help you if you help me!)

Thus if you start with a network without many (reciprocal) ties it would be very difficult to get more reciprocal ties in the normal model. However, with simultaneity this should be possible.

3.1.1. Simulate networks

NSIM <- 500
STATS <- list(ts_degree, ts_recip)
STARTS <- c(10, -1,2)

sims1 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(1,0,0), verbose  = FALSE, parallel = TRUE) #ministep

sims2 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), verbose  = FALSE, parallel = TRUE) #twostep: simultaneity

sims3 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, dist2 = 2, verbose  = FALSE, parallel = TRUE)   #twostep: weak coordination

sims4 <-  ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #twostep: strict coordination

sims5 <-  ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,0,1), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #simstep: one actor two ministeps

3.1.2. Counting dyads

df1 <- ts_dyads(sims=sims1, simtype="ministep")
df2 <- ts_dyads(sims=sims2, simtype="twostep: simultaneity")  
df3 <- ts_dyads(sims=sims3, simtype="twostep: weak coordination")  
df4 <- ts_dyads(sims=sims4, simtype="twostep: strict coordination")  
df5 <- ts_dyads(sims=sims5, simtype="simstep")  

df <- rbind(df1, df2, df3, df4, df5)

3.1.3. Plot results of dyadcensus

p <- ggplot(df, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "dyad type", y = "dyad count", fill="simulation type")
  
p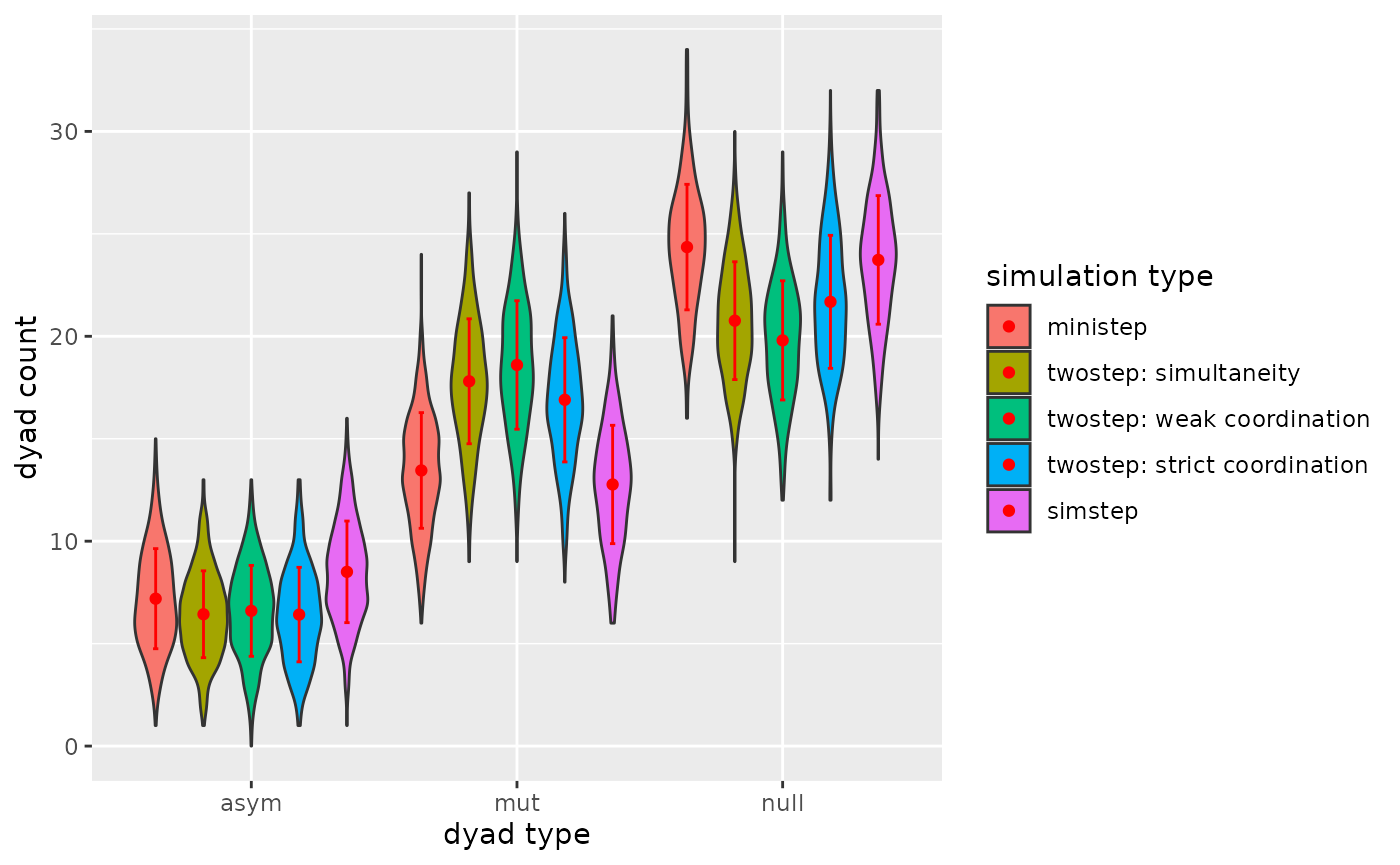

Figure 3.1.3. Dyadcensus Model 1

3.1.4. Conclusion

Yes, if you allow simultaneity, we will observe more reciprocal ties after same number of possible tie-changes.

Perhaps the model with ministeps only would reach the same target values (for dyads) but probably by using more possible tie-changes. This would mean there will be more noise in the network chains, this can/will have results for other network statistics.

Also note, that if you make the network larger, simultaneity will less likely to be different from two consecutive ministeps, this is because the two agents do not influence each others evaluation functions.

3.2. Model 2: Degree, reciprocity, transTrip

Let us assume people really don’t like to have a non-reciprocal tie but do like reciprocal ties a lot and do favor transitivity.

Is it unlikely that a transitive triad will emerge if we have coordination, because for one of the actors will not evaluate the transitive triad positively because in wrong position. Or, because reciprocal ties are more likely when actors coordinate, we will also observe more transitive triads.

3.2.1. Simulate networks

NSIM <- 500
STATS <- list(ts_degree, ts_recip,ts_transTrip)
STARTS <- c(10, -1, 2, 1)

sims1 <- ts_sims(startvalues = STARTS , net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(1,0,0), verbose  = FALSE, parallel = TRUE) #ministep

sims2 <- ts_sims(startvalues = STARTS , net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), verbose  = FALSE, parallel = TRUE) #twostep: simultaneity

sims3 <- ts_sims(startvalues = STARTS , net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, dist2 = 2, verbose  = FALSE, parallel = TRUE)   #twostep: weak coordination

sims4 <-  ts_sims(startvalues = STARTS , net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #twostep: strict coordination

sims5 <-  ts_sims(startvalues = STARTS , net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,0,1), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #simstep: one actor two ministeps

3.2.2. Counting dyads

df1 <- ts_dyads(sims=sims1, simtype="ministep")
df2 <- ts_dyads(sims=sims2, simtype="twostep: simultaneity")  
df3 <- ts_dyads(sims=sims3, simtype="twostep: weak coordination")  
df4 <- ts_dyads(sims=sims4, simtype="twostep: strict coordination")  
df5 <- ts_dyads(sims=sims5, simtype="simstep")  

df <- rbind(df1, df2, df3, df4, df5)

3.2.3. Plot results of the dyadcensus

p <- ggplot(df, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "dyad type", y = "dyad count", fill="simulation type")
  
p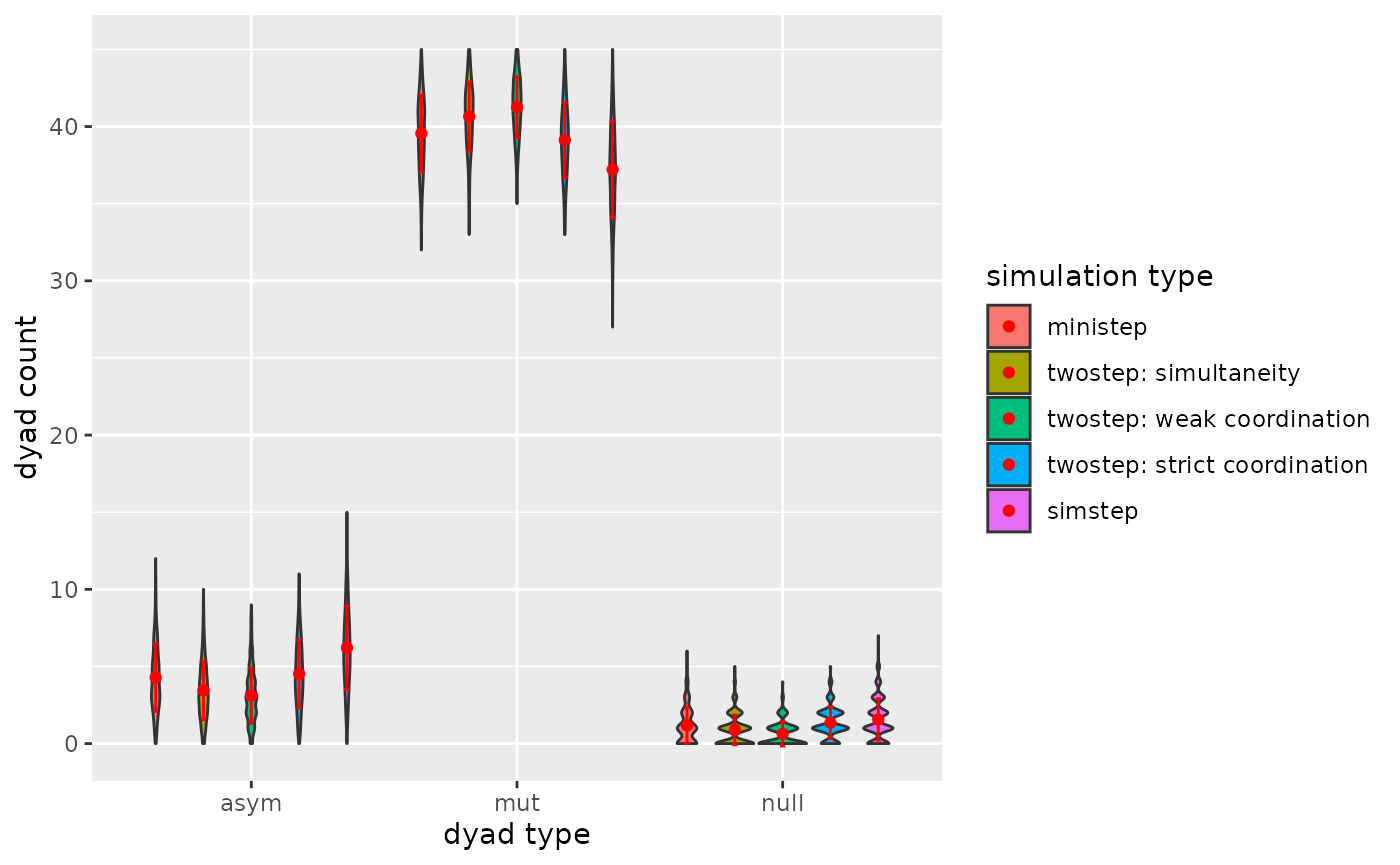

Figure 3.2.3. Dyadcensus Model 2

3.2.4. Counting triads

df1 <- ts_triads(sims=sims1, simtype="ministep")
df2 <- ts_triads(sims=sims2, simtype="twostep: simultaneity")  
df3 <- ts_triads(sims=sims3, simtype="twostep: weak coordination")  
df4 <- ts_triads(sims=sims4, simtype="twostep: strict coordination")  
df5 <- ts_triads(sims=sims5, simtype="simstep")  

df <- rbind(df1, df2, df3, df4, df5)

3.2.5. Plot results of the triadcensus

Intermezzo

The different triad configurations may embed one or more transitive triads. This is my quick count:

030T: 1

120U: 1

120D: 2

120C: 2

210: 4

300: 6


dftest <- df[df$x=="030T" | df$x=="120U", ]
p1 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")

p1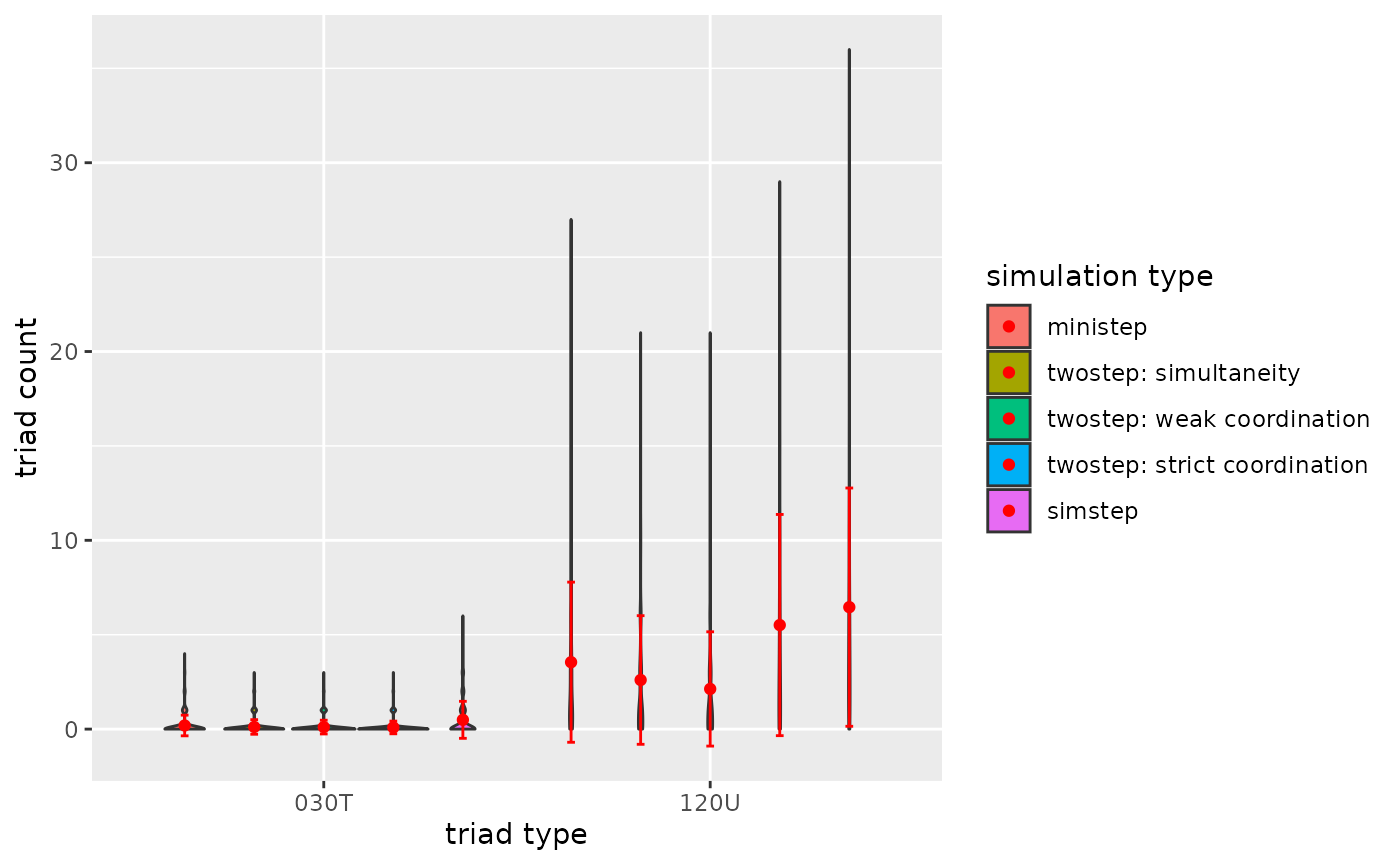

Figure 3.2.5a. Triadcensus Model 2 (Triads 030T & 120U)

dftest <- df[df$x=="120D" | df$x=="120C" , ]
p2 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")

p2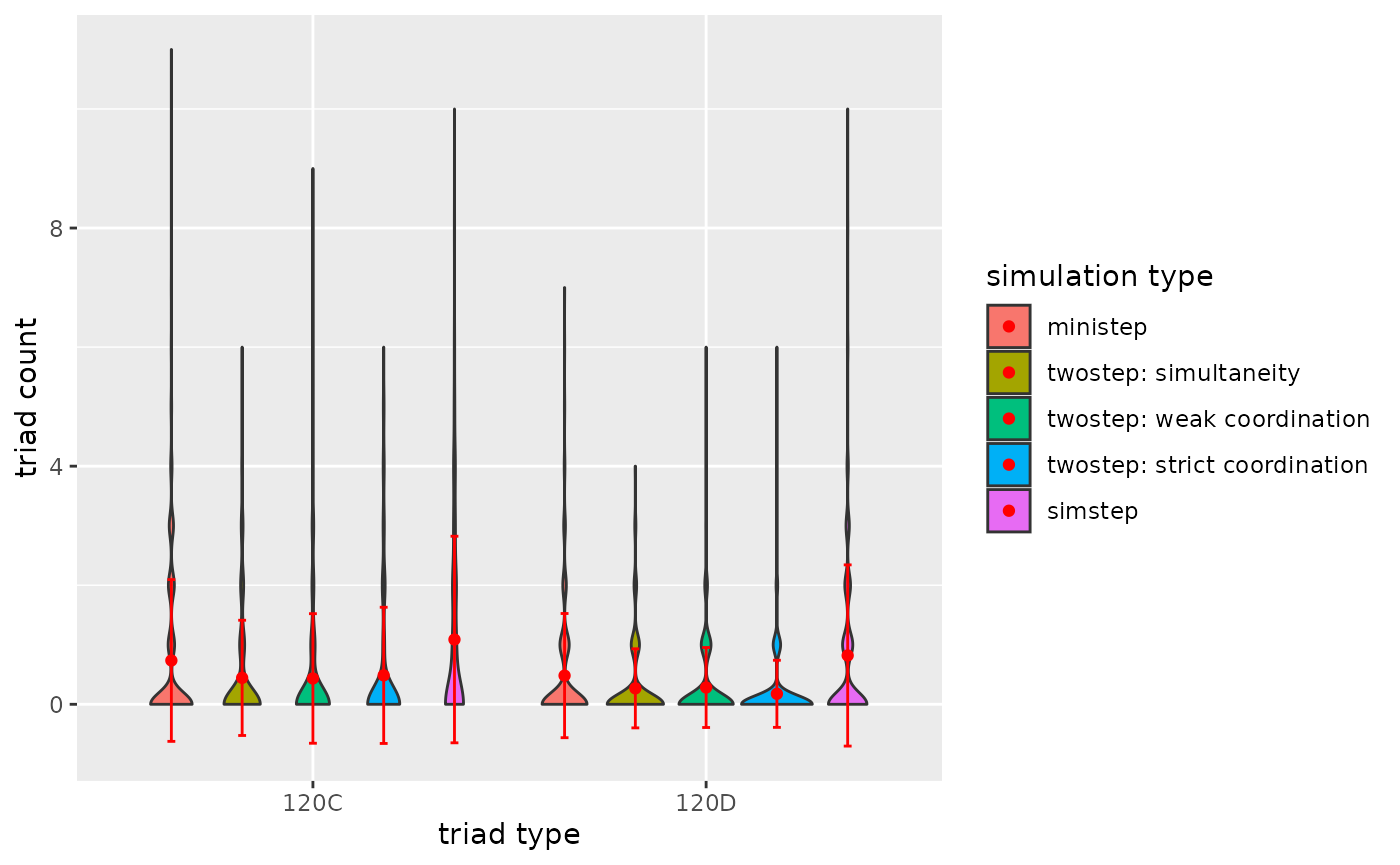

Figure 3.2.5b. Triadcensus Model 2 (Triads 120D & 120C)

dftest <- df[df$x=="210" | df$x=="300" , ]
p3 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")

p3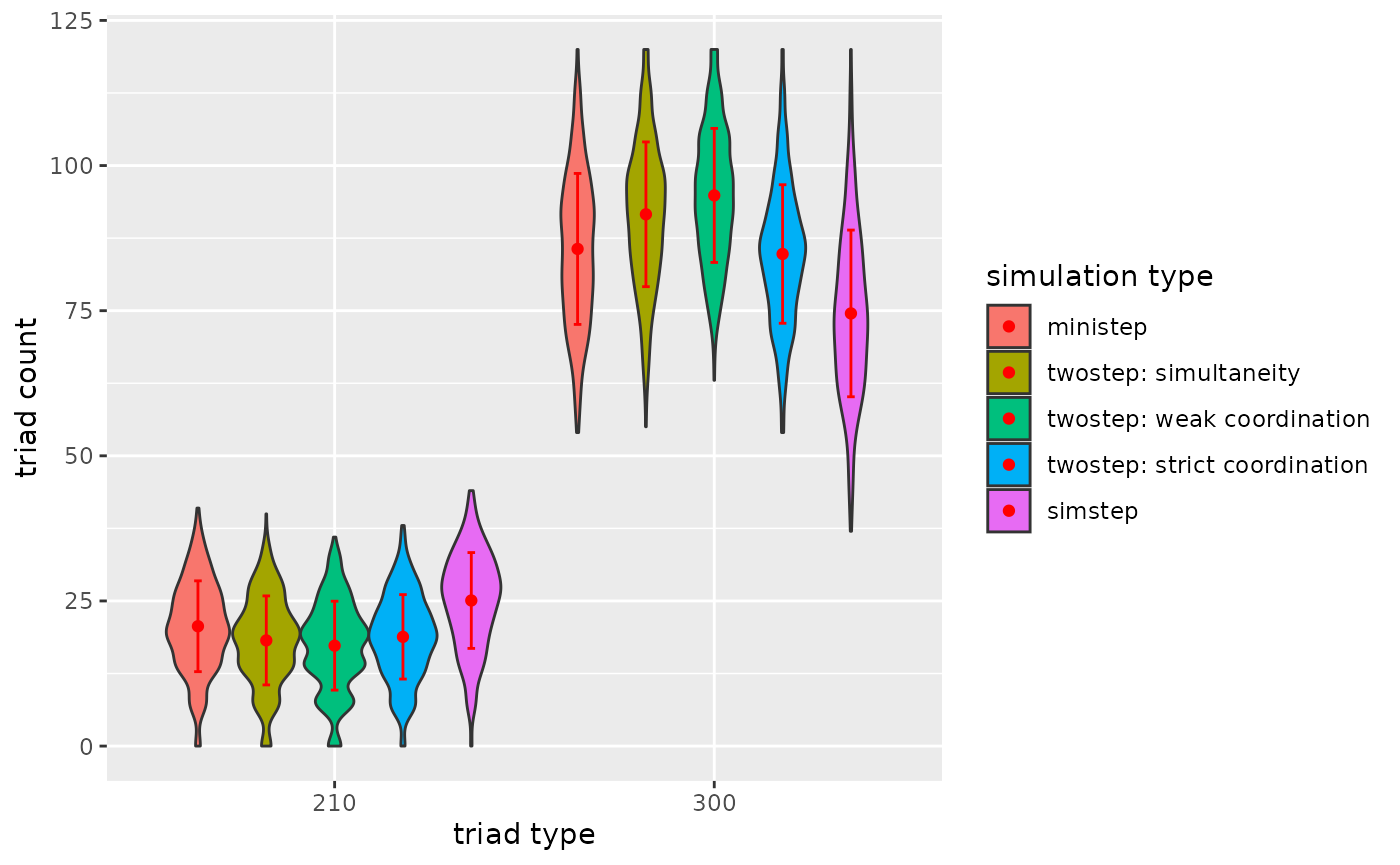

Figure 3.2.5c. Triadcensus Model 2 (Triads 210 & 300)

3.2.6. Conclusion

For this network (ts_net1) and given the network statistics degree, reciprocity and transitivity…

A general conclusion is that the type of ABM does impact the dyad and triad count after the simulation run.
A tentative conclusion would be that weak coordination impacts (complex) triad configurations more than strict coordination, because under weak coordination asymmetric dyads are plausible.

3.3. Model 3: Degree, reciprocity, transTrip, transMedTrip

Let us assume people really don’t like to have a non-reciprocal tie but do like reciprocal ties a lot and do favor transitivity.

It is now likely that a transitive triad will emerge if we have coordination, because one of the actors evaluate the transTrip and the other may positively evaluate transMedTrip positively.

3.3.1. Simulate networks

NSIM <- 500
STATS <- list(ts_degree, ts_recip, ts_transTrip, ts_transMedTrip)
STARTS <- c(10, -2 ,1 ,2 ,2)

sims1 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(1,0,0), verbose  = FALSE, parallel = TRUE) #ministep

sims2 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), verbose  = FALSE, parallel = TRUE) #twostep: simultaneity

sims3 <- ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, dist2 = 2, verbose  = FALSE, parallel = TRUE)   #twostep: weak coordination

sims4 <-  ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,1,0), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #twostep: strict coordination

sims5 <-  ts_sims(startvalues = STARTS, net = ts_net1, statistics = STATS, nsims = NSIM, p2step = c(0,0,1), dist1 = 2, verbose  = FALSE, parallel = TRUE)  #simstep: one actor two ministeps

3.3.2. Counting dyads

df1 <- ts_dyads(sims=sims1, simtype="ministep")
df2 <- ts_dyads(sims=sims2, simtype="twostep: simultaneity")  
df3 <- ts_dyads(sims=sims3, simtype="twostep: weak coordination")  
df4 <- ts_dyads(sims=sims4, simtype="twostep: strict coordination")  
df5 <- ts_dyads(sims=sims5, simtype="simstep") 

df <- rbind(df1, df2, df3, df4, df5)

3.3.3. Plot results of the dyadcensus

p <- ggplot(df, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "dyad type", y = "dyad count", fill="simulation type")
  
p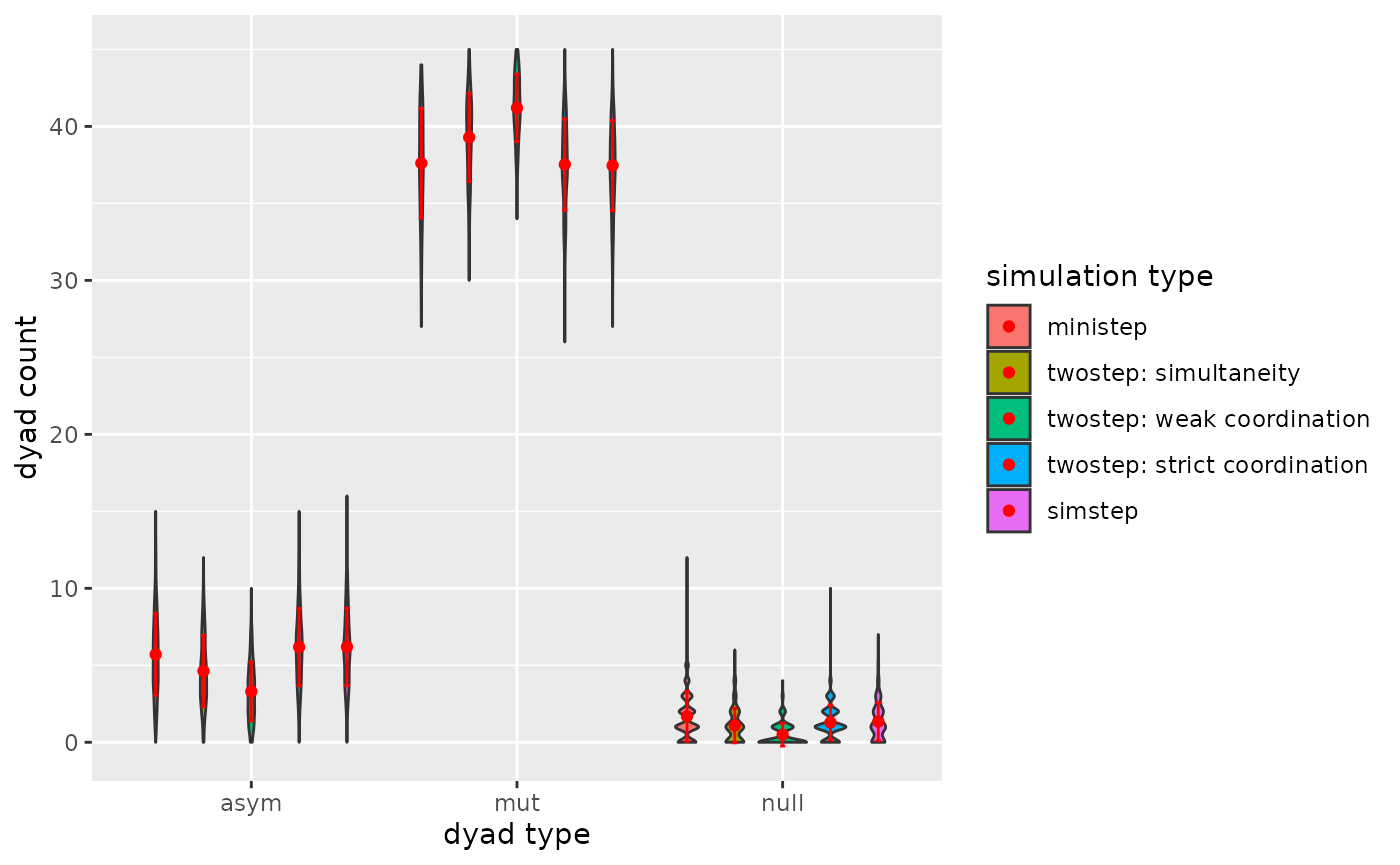

Figure 3.3.3. Dyadcensus Model 3

3.3.4. Counting triads

df1 <- ts_triads(sims=sims1, simtype="ministep")
df2 <- ts_triads(sims=sims2, simtype="twostep: simultaneity")  
df3 <- ts_triads(sims=sims3, simtype="twostep: weak coordination")  
df4 <- ts_triads(sims=sims4, simtype="twostep: strict coordination")  
df5 <- ts_triads(sims=sims5, simtype="simstep")  

df <- rbind(df1, df2, df3, df4, df5)

3.3.5. Plot results of the triadcensus

dftest <- df[df$x=="030T" | df$x=="120U", ]
p1 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep"))))+ 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")
p1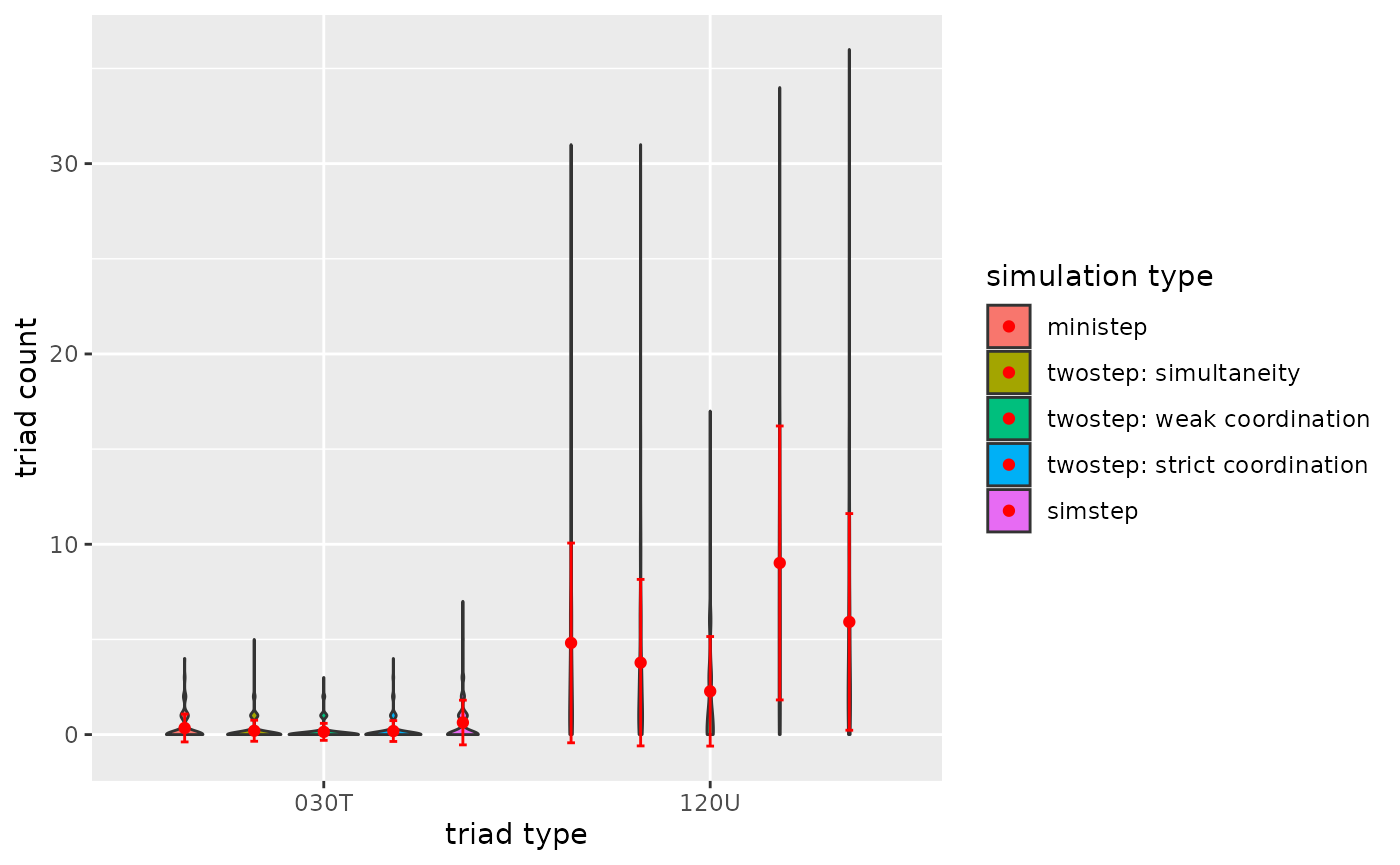

Figure 3.3.5a. Triadcensus Model 3 (Triads 030T & 120U)

dftest <- df[df$x=="120D" | df$x=="120C" , ]
p2 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")
p2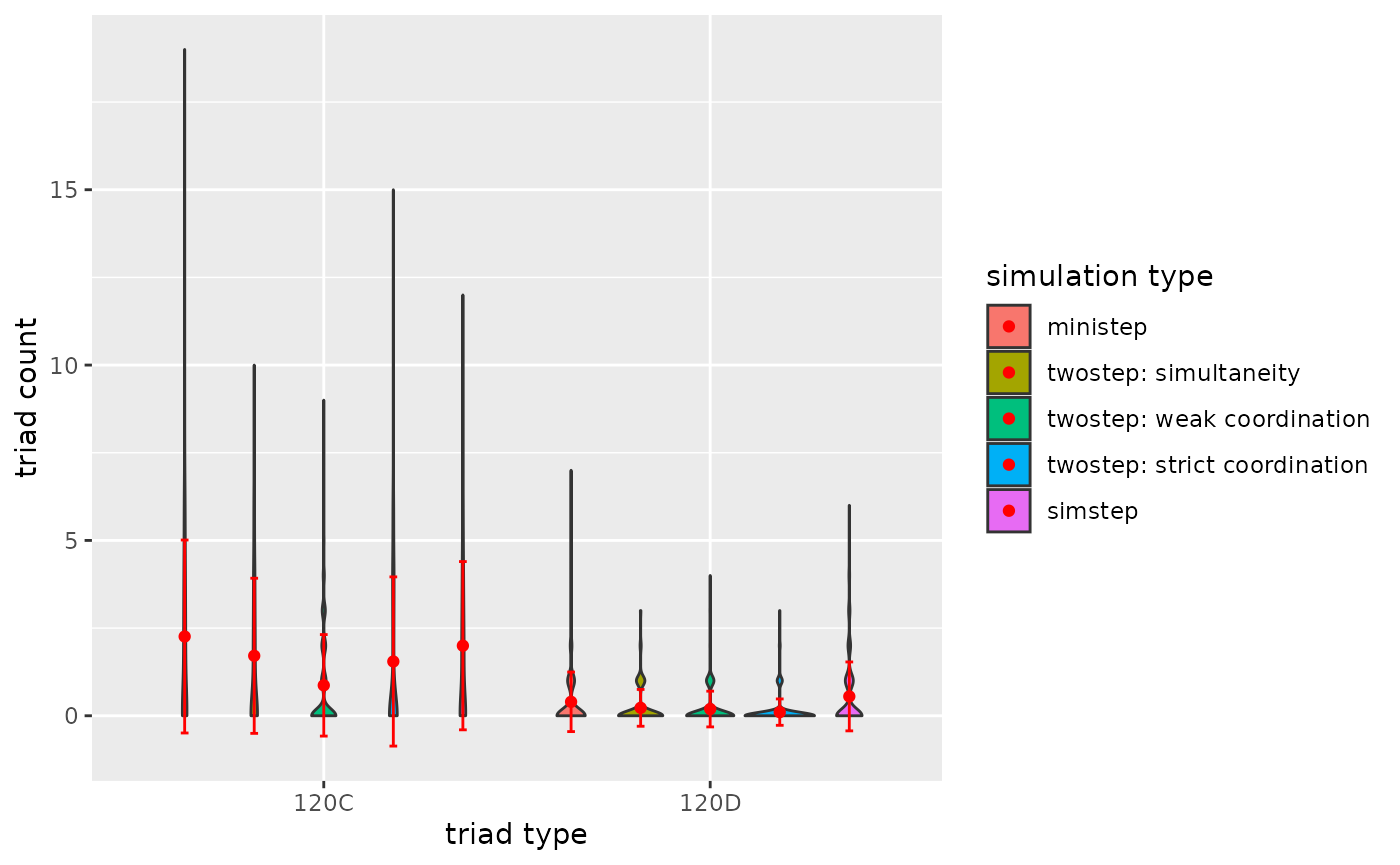

Figure 3.2.5b. Triadcensus Model 3 (Triads 120D & 120C)

dftest <- df[df$x=="210" | df$x=="300" , ]
p3 <- ggplot(dftest, aes(x=x, y=y, fill=factor(type, levels=c("ministep", "twostep: simultaneity", "twostep: weak coordination", "twostep: strict coordination", "simstep")))) + 
  geom_violin(position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "errorbar",
               fun.max = function(x) mean(x) + sd(x),
               fun.min = function(x) mean(x) - sd(x),
               width=.1,
               color="red", position=position_dodge(.9)) + 
  stat_summary(fun = mean,
               geom = "point",
               color="red", position=position_dodge(.9)) +
  labs(x = "triad type", y = "triad count", fill="simulation type")

p3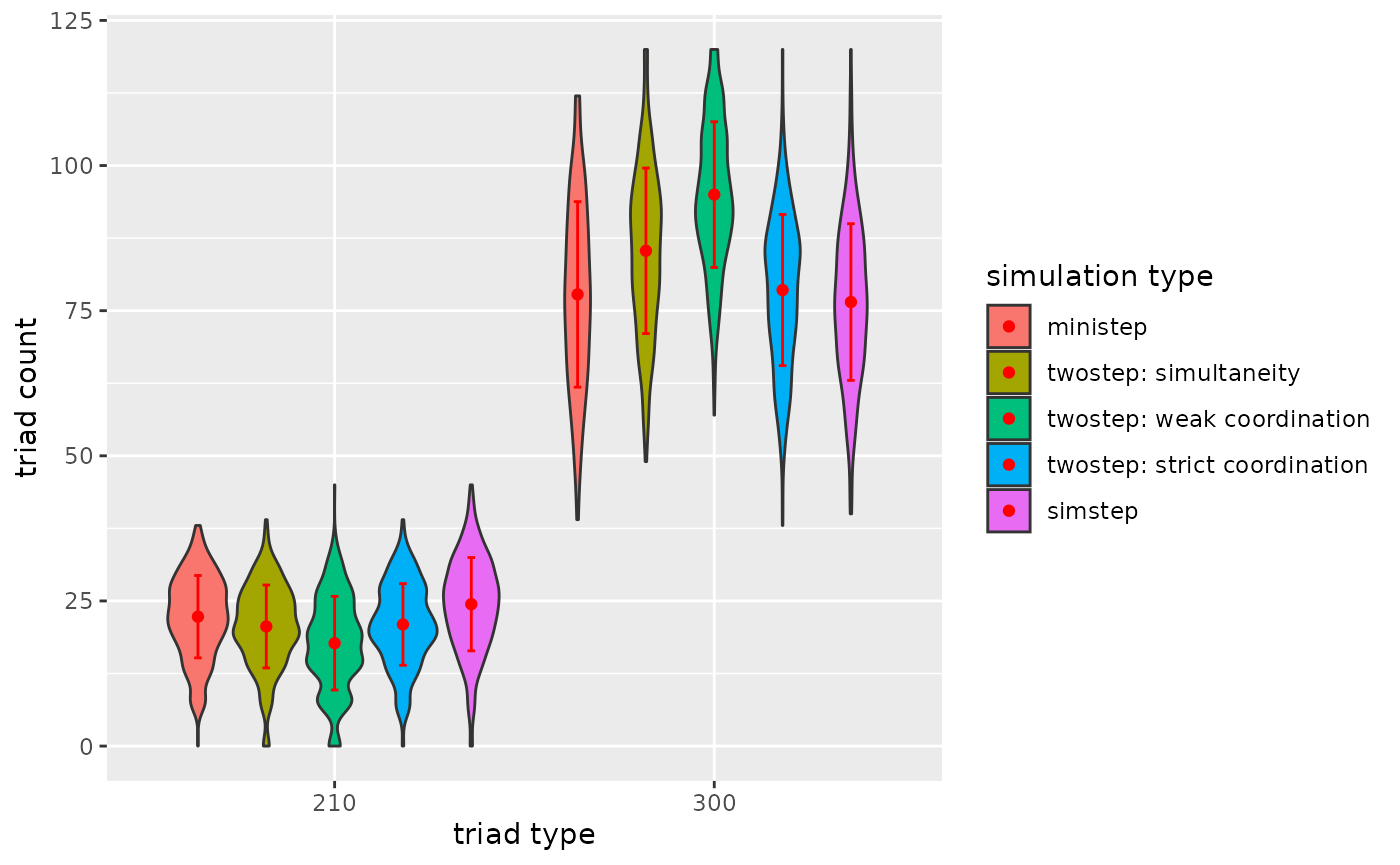

Figure 3.2.5c. Triadcensus Model 3 (Triads 210 & 300)

3.3.6. Conclusion

For this network (ts_net1) and given the network statistics degree, reciprocity, transitivity and mediated transitivity…

It is clearly strict coordination that leads to diverging dyad and triad counts.
I tentatively conclude that, as expected, transitive triads are more common under coordination.
I tentatively conclude that especially strict coordination leads to transitive triads (except triads 210 and 300).

4. Conclusion

The different ABMs may give a different dyad and triad count (given the same start network and network statistics).
Which ABM leads to the most diverging dyad and triad count depends on the included network statistics.
It is difficult to predict (complexity!) how the results of the ABMs will diverge a priori.