Chapter 3 Methods
3.1 Causes
When testing hypotheses on assortative mating many methodological approaches can be used. We may predict the frequency of specific dyads in our population with loglinear models and the data we use is commonly structured in a square table like the one below. Loglinear models are, in essence, nothing more than a nice, parsimonious and fancy way to calculate odds ratio’s. If we have a small, well filled table of just a few attributes, loglinear models are considered to be the golden standard.
| Wife educ-high | Wife educ-low | |
|---|---|---|
| Husband educ-high | 350 | 150 |
| Husband educ-low | 200 | 400 |
Another approach is to take the characteristics of the dyad (e.g. 1 = intermarriage and 0 = no intermarriage) as the dependent variable. This dependent variable can than be explained by applying (conditional) (multinomial) logistic regression techniques. In this case, the data is commonly structured in long format and looks something like the table below.
| dyad_id | wife educ | wife age | husband educ | husband age | intermarriage |
|---|---|---|---|---|---|
| 1 | LOW | 30.63 | LOW | 26.91 | 0 |
| 2 | LOW | 24.79 | LOW | 34.61 | 0 |
| 3 | HIGH | 19.00 | HIGH | 25.92 | 0 |
| 4 | HIGH | 29.31 | LOW | 39.08 | 0 |
| 5 | HIGH | 25.32 | LOW | 30.11 | 0 |
| 6 | LOW | 23.86 | LOW | 19.01 | 0 |
| 7 | HIGH | 36.36 | LOW | 35.34 | 0 |
| 8 | LOW | 35.58 | HIGH | 22.64 | 0 |
| 9 | LOW | 24.24 | HIGH | 36.36 | 0 |
| 10 | LOW | 20.27 | HIGH | 20.79 | 0 |
| 11 | HIGH | 24.08 | LOW | 34.20 | 0 |
| 12 | HIGH | 44.44 | LOW | 23.97 | 0 |
| 13 | LOW | 33.40 | LOW | 25.77 | 0 |
| 14 | HIGH | 27.86 | HIGH | 35.55 | 0 |
| 15 | LOW | 21.97 | HIGH | 19.44 | 0 |
| 16 | HIGH | 38.16 | LOW | 18.42 | 0 |
| 17 | HIGH | 44.85 | HIGH | 37.86 | 0 |
| 18 | LOW | 30.91 | LOW | 23.21 | 0 |
| 19 | HIGH | 24.30 | HIGH | 31.53 | 0 |
| 20 | LOW | 36.19 | LOW | 21.50 | 0 |
Which methodology is preferred should depend on your hypotheses and on the data you have to your availability.
Please be aware that in both approaches we normally do not have information on (the frequency or characteristics of) dyads in which there is no relation between ego and alter. Thus, you may have information on characteristics of me and my wife but you do not have information on all other women (or men) I could have married but didn’t. I fished my wife out of the sea but we don’t know what the other fish looked like. (Luckily my wife is no scientist and won’t read this clarification.)
3.2 Consequences
The method used to explain consequences of dyads depends on our Unit of Analysis. If it is the dyad itself (e.g. mean relationship quality) methods are relatively straightforward, because we may assume that the observations at the dyad-level are independent. We may explain this dyad-characteristic by other characteristics of the dyad (e.g. length of marriage) and by characteristics of each spouse (e.g. working hours men, working hours woman).4 That characteristics of the spouses, the covariates, are correlated does not necessarily pose a big problem.5
If, on the other hand, the unit of analysis are the partners themselves who make up the dyad, we need to acknowledge that the observations between the partners of the same couple are not independent. In part exactly because partners select and influence each other and share a social context. One solution could be to simply randomly select one partner of each couple or, if partners can be clearly distinguished - for example men and women in heterosexual couples - the different partners could be analyzed separately. A disadvantage of the latter two approaches is, however, that the covariance between the partners cannot be explained anymore, although this may exactly be the focus of our research questions. A more elegant solution, is to take the interdependencies into account and model these explicitly. This can be done within a multi-level framework and within a structural-equation modelling framework.
3.3 Research questions
When we discussed the methods to analyze causes of homogamy, we were interested in homophily within couples at one point in time and focused on selection as explanans. Now, when we are discussing the consequences of dyads, we are interested in explaining trends in homophily within couples - thus homophily as a consequence of mating - and focus on shared context and influence processes as explanans.
Naturally, because we are interested in trends in homophily within couples, we focus on dynamic characteristics of the spouses. Thus not, ethnicity, or educational attainment, but, for example, on their political opinions.
Let us suppose our aim is to write a scientific paper on political opinion homophily within couples. We will formulate the following research questions:
- To what extent can we observe trends in political opinion homophily (or opinion similarity) within couples?
- To what extent can we explain trends in political opinion homophily by influence processes taking place between spouses?
- To what extent can we explain trends in political opinion homophily by the shared (social) context of the couple?
Perhaps, you also want to focus in this paper on the influence process itself and formulate a second set of research questions:
- To what extent are influence process within couples influenced by (or conditional on):
- the shared context?
- characteristics of the couple?
- characteristics of the spouses?
- the shared context?
3.4 Data
We will use the data from the LISS panel.
More concretely, we will use:
- 11 waves (2008-2014, 2016-2029)
- Filter on heterosexual couples (cohabiting and married)
- Filter on couples of which both spouses are older than 25.
We have already constructed a dataset for you guys and gals to work with which contains information on more than 3000 couples. Don’t forget it is a panel data set. This means we have more observations for the same couple (and spouses) over time. Also be aware that our spouses can be clearly distinguished from one another (i.e. husband versus wife).
Please download this data file to your working directory.
3.4.1 Variables
Variables of interest and value labels:
- education: = highest completed education in years (4-16.5)
- sex: = 0 = male / 1 = female
- eu_integration: 0 = eu integration has gone too far / 4 = eu integration should go further
- immigrants: 0 = immigrants should adjust / 4 immigrants can retain their own culture.
- euthanasia: 1 = euthanasia should be forbidden / 5 euthanasia should be permitted
- income_diff: 1 differences in income should increase / 5 differences in income should decrease
For the original variables in Dutch see below:
opleiding
Hoogste opleiding met diploma
1 basisonderwijs
2 vmbo
3 havo/vwo
4 mbo
5 hbo
6 wo
7 anders
8 (Nog) geen onderwijs afgerond
9 Volgt nog geen onderwijs
Hierbij hebben wij opleiding gecategoriseerd in drie groepen:
1. Laag: basisonderwijs en vmbo
2. Midden: havo/vwo en mbo
3. Hoog: hbo en wo
We nemen enkel mensen van 25 jaar en ouder mee. Van hen verwachten we dat ze klaar zijn met hun onderwijscarriere.
EU integratie
De Europese integratie is te ver gegaan.
1 Helemaal oneens
2 Oneens
3 Niet eens, niet oneens
4 Eens
5 Helemaal eens
Migratie/integratie
In Nederland vinden sommigen dat mensen met een migratie achtergrond hier moeten kunnen leven met behoud van de eigen cultuur. Anderen vinden dat zij zich geheel moeten aanpassen aan de Nederlandse cultuur. Waar zou u uzelf plaatsen op een schaal van 1 t/m 5, waarbij 1 behoud van eigen cultuur voor mensen met een migratie achtergrond betekent en 5 dat zij zich geheel moeten aanpassen?
1 behoud van eigen cultuur voor mensen met een migratie achtergrond
2
3
4
5 mensen met een migratie achtergrond moeten zich geheel aanpassen
3.5 Descriptives
3.5.1 Preperation
#### clean the environment ####.
rm(list = ls())
#### packages ####.
require(tidyverse)
##### Data input ###.
load("addfiles/partner_dataprepped.Rdata")
# clean a little bit.
rm("partner_df_wide") #we will make a wide file later again.
partner_df_long <- partner_df_long %>%
rename(dyad_id = "nohouse_encr") %>%
select(-c("hetero", "n", "nomem_encr.m", "positie.m", "nomem_encr.f", "positie.f"))
partner_df_wide <- reshape(partner_df_long, direction = "wide", idvar = "dyad_id", timevar = "time")Please note that our time variable indicates survey year. We do not want to describe period trends in opinion homophily within couples but lifecourse trends. We will call the latter the within-trend. For people familiar with life course research, hopefully you will see the resemblance to the Age-Period-Cohort conundrum. We therefore need to construct a time_within variable and add it to our data set.
Before copying the ‘hidden code’ below, please try to do this yourself.
Now we need to think of how we want to operationalize opinion homophily.
The stronger the political opinion homophily within couples, the larger the spousal correspondence, the larger the association between the opinions of the partners. We discussed covariance and correlations here. Would that be an option?
A different approach would be to operationalize increasing homophily as decreasing absolute opinion dissimilarity between the spouses (Iyengar, Konitzer, and Tedin 2018).
3.5.2 Opinion homophily over within-time
Let’s have a go.
cors <- partner_df_long %>%
group_by(within_time) %>% #we want to see within couple trends.
group_map(~ cor.test(x=.x$immigrants.m, y=.x$immigrants.f)$estimate ) %>%
unlist()
# How to do this in Base R?
# # we subset the data.
# cor.test(partner_df_long$immigrants.m[partner_df_long$within_time==1], partner_df_long$immigrants.f[partner_df_long$within_time==1])
#
# #And we could use a loop.
# cors <- list()
# for (i in 1:11) {
# cors[[i]] <- cor.test(partner_df_long$immigrants.m[partner_df_long$within_time==i], partner_df_long$immigrants.f[partner_df_long$within_time==i])
# }
covs <- partner_df_long %>%
group_by(within_time) %>% #we want to see within couple trends.
group_map(~ cov(x=.x$immigrants.m, y=.x$immigrants.f, use="complete.obs") ) %>%
unlist()
partner_df_long %>%
mutate(distance = abs(immigrants.m - immigrants.f)) %>%
group_by(within_time) %>% #we want to see within couple trends.
summarise(mean_dist = mean(distance, na.rm=T)) %>%
add_column(cors) %>%
add_column(covs)#> # A tibble: 11 × 4
#> within_time mean_dist cors covs
#> <dbl> <dbl> <dbl> <dbl>
#> 1 1 0.716 0.440 0.422
#> 2 2 0.711 0.450 0.431
#> 3 3 0.706 0.438 0.402
#> 4 4 0.662 0.485 0.446
#> 5 5 0.657 0.488 0.450
#> 6 6 0.670 0.483 0.452
#> 7 7 0.675 0.458 0.416
#> 8 8 0.681 0.432 0.374
#> 9 9 0.686 0.442 0.399
#> 10 10 0.662 0.419 0.328
#> 11 11 0.650 0.474 0.383Whow! Please look at the above results for at least 5 minutes before you move one. What is your interpretation? Do you observe a (significant) trend? Suppose that the mean distance indeed decreased but that, as a consequence, also the variance in this opinion decreased. What impact would this have for the covariance?
3.5.3 Distinguishing period trends from lifecourse trends
The above results are hard to interpret. In part because we mix up period trends and and within-trends. And although we are interested in influence and shared context effects, we must not forget about (de)selection effects. The couples who survive to reach within-time 11 are probably a selective subgroup of all couples.
A bit more sophisticated:
- calculate the (euclidean) distance between all four attitudes.
- Try to distinguishing period trends from lifecourse trends.
- Try to take into account of selective sample attrition.6
trends <- partner_df_long %>%
filter(n_time>4) %>% #trying to take selective sample attrition into account.
mutate(distance = sqrt((immigrants.m - immigrants.f)^2 + (euthanasia.m - euthanasia.f)^2 + (income_diff.m - income_diff.f)^2 + (eu_integration.m - eu_integration.f)^2 )) %>% #euclidean distance of four political opinions
group_by(start_time, within_time) %>% #we want to see within couple trends but need to 'control for' period trends
summarise(mean_dist = mean(distance, na.rm=T))
#Put results in a matrix
#?? how to do this the tidy way?
trends_matrix <- matrix(NA, nrow=11, ncol=11)
for (i in 1:length(trends$start_time)) {
trends_matrix[trends$start_time[i],trends$within_time[i]] <- trends$mean_dist[i]
}
rownames(trends_matrix) <- c(2008:2014, 2016:2019)
colnames(trends_matrix) <- paste("within_time", 1:11, sep="_")
trends_matrix| within_time_1 | within_time_2 | within_time_3 | within_time_4 | within_time_5 | within_time_6 | within_time_7 | within_time_8 | within_time_9 | within_time_10 | within_time_11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 1.929 | 1.922 | 1.793 | 1.809 | 1.793 | 1.72 | 1.720 | 1.777 | 1.815 | 1.843 | 1.816 |
| 2009 | 2.009 | 1.743 | 1.619 | 1.842 | 1.719 | 1.681 | 1.636 | 1.743 | 1.640 | 1.874 | NA |
| 2010 | 1.823 | 1.798 | 1.827 | 1.691 | 1.811 | 1.697 | 1.699 | 1.861 | 1.776 | NA | NA |
| 2011 | 2.072 | 1.803 | 1.931 | 1.549 | 1.829 | 2.035 | 1.466 | 1.973 | NA | NA | NA |
| 2012 | 1.826 | 1.721 | 1.588 | 1.799 | 1.848 | 1.581 | 1.724 | NA | NA | NA | NA |
| 2013 | 1.908 | 1.932 | 1.669 | 1.98 | 1.883 | 1.744 | NA | NA | NA | NA | NA |
| 2014 | 1.945 | 1.959 | 1.981 | 1.693 | 1.999 | NA | NA | NA | NA | NA | NA |
| 2016 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 2017 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 2018 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 2019 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
Follow the same couples over time by following the diagonals (e.g. the blue and red).
What would you conclude?
3.6 Analysis
Even tough the above descriptives do not show convincing time trends, we know that partners may still influence each other. Let us try to test for influence processes.
Feel free to re-estimate all models yourself. But it will be way quicker to download all results.
3.6.1 Preperation
We need to do some additional dataprep.
I know it is a bit cumbersome, but we will make a datafile for each dependent variable separately and will use some shorter names. The data files are stored in a list called datalist_ori.
datalist_ori <- list()
# dep1: eu_integration
dat <- data.frame(x1 = partner_df_wide$eu_integration.m.1)
dat$x2 <- partner_df_wide$eu_integration.m.2
dat$x3 <- partner_df_wide$eu_integration.m.3
dat$x4 <- partner_df_wide$eu_integration.m.4
dat$x5 <- partner_df_wide$eu_integration.m.5
dat$x6 <- partner_df_wide$eu_integration.m.6
dat$x7 <- partner_df_wide$eu_integration.m.7
dat$x8 <- partner_df_wide$eu_integration.m.8
dat$x9 <- partner_df_wide$eu_integration.m.9
dat$x10 <- partner_df_wide$eu_integration.m.10
dat$x11 <- partner_df_wide$eu_integration.m.11
dat$y1 <- partner_df_wide$eu_integration.f.1
dat$y2 <- partner_df_wide$eu_integration.f.2
dat$y3 <- partner_df_wide$eu_integration.f.3
dat$y4 <- partner_df_wide$eu_integration.f.4
dat$y5 <- partner_df_wide$eu_integration.f.5
dat$y6 <- partner_df_wide$eu_integration.f.6
dat$y7 <- partner_df_wide$eu_integration.f.7
dat$y8 <- partner_df_wide$eu_integration.f.8
dat$y9 <- partner_df_wide$eu_integration.f.9
dat$y10 <- partner_df_wide$eu_integration.f.10
dat$y11 <- partner_df_wide$eu_integration.f.11
# treat education as a time stable. And use all available data.
dat$oplx <- rowMeans(partner_df_wide[, c("oplmet.m.1", "oplmet.m.2", "oplmet.m.3", "oplmet.m.4", "oplmet.m.5",
"oplmet.m.6", "oplmet.m.7", "oplmet.m.8", "oplmet.m.9", "oplmet.m.10", "oplmet.m.11")], na.rm = T)
dat$oply <- rowMeans(partner_df_wide[, c("oplmet.f.1", "oplmet.f.2", "oplmet.f.3", "oplmet.f.4", "oplmet.f.5",
"oplmet.f.6", "oplmet.f.7", "oplmet.f.8", "oplmet.f.9", "oplmet.f.10", "oplmet.f.11")], na.rm = T)
# calculate diff in education between men and women
dat$oplxy <- dat$oplx - dat$oply
# table(dat$oplx, dat$oply, useNA = 'always') hist(dat$oplxy)
# define three groups for multigroup analyses
dat$oplgroup <- ifelse(dat$oplxy > 1, "menhigher", NA)
dat$oplgroup <- ifelse(dat$oplxy < -1, "womenhigher", dat$oplgroup)
dat$oplgroup <- ifelse(dat$oplxy <= 1 & dat$oplxy >= -1, "equal", dat$oplgroup)
# table(dat$oplgroup, useNA = 'always')
dat_ori <- dat
datalist_ori[[1]] <- dat_ori
# dep2: immigrants
dat <- data.frame(x1 = partner_df_wide$immigrants.m.1)
dat$x2 <- partner_df_wide$immigrants.m.2
dat$x3 <- partner_df_wide$immigrants.m.3
dat$x4 <- partner_df_wide$immigrants.m.4
dat$x5 <- partner_df_wide$immigrants.m.5
dat$x6 <- partner_df_wide$immigrants.m.6
dat$x7 <- partner_df_wide$immigrants.m.7
dat$x8 <- partner_df_wide$immigrants.m.8
dat$x9 <- partner_df_wide$immigrants.m.9
dat$x10 <- partner_df_wide$immigrants.m.10
dat$x11 <- partner_df_wide$immigrants.m.11
dat$y1 <- partner_df_wide$immigrants.f.1
dat$y2 <- partner_df_wide$immigrants.f.2
dat$y3 <- partner_df_wide$immigrants.f.3
dat$y4 <- partner_df_wide$immigrants.f.4
dat$y5 <- partner_df_wide$immigrants.f.5
dat$y6 <- partner_df_wide$immigrants.f.6
dat$y7 <- partner_df_wide$immigrants.f.7
dat$y8 <- partner_df_wide$immigrants.f.8
dat$y9 <- partner_df_wide$immigrants.f.9
dat$y10 <- partner_df_wide$immigrants.f.10
dat$y11 <- partner_df_wide$immigrants.f.11
# treat education as a time stable. And use all available data.
dat$oplx <- rowMeans(partner_df_wide[, c("oplmet.m.1", "oplmet.m.2", "oplmet.m.3", "oplmet.m.4", "oplmet.m.5",
"oplmet.m.6", "oplmet.m.7", "oplmet.m.8", "oplmet.m.9", "oplmet.m.10", "oplmet.m.11")], na.rm = T)
dat$oply <- rowMeans(partner_df_wide[, c("oplmet.f.1", "oplmet.f.2", "oplmet.f.3", "oplmet.f.4", "oplmet.f.5",
"oplmet.f.6", "oplmet.f.7", "oplmet.f.8", "oplmet.f.9", "oplmet.f.10", "oplmet.f.11")], na.rm = T)
# calculate diff in education between men and women
dat$oplxy <- dat$oplx - dat$oply
# table(dat$oplx, dat$oply, useNA = 'always') hist(dat$oplxy)
# define three groups for multigroup analyses
dat$oplgroup <- ifelse(dat$oplxy > 1, "menhigher", NA)
dat$oplgroup <- ifelse(dat$oplxy < -1, "womenhigher", dat$oplgroup)
dat$oplgroup <- ifelse(dat$oplxy <= 1 & dat$oplxy >= -1, "equal", dat$oplgroup)
# table(dat$oplgroup, useNA = 'always')
dat_ori <- dat
datalist_ori[[2]] <- dat_ori
# dep3: euthanasia
dat <- data.frame(x1 = partner_df_wide$euthanasia.m.1)
dat$x2 <- partner_df_wide$euthanasia.m.2
dat$x3 <- partner_df_wide$euthanasia.m.3
dat$x4 <- partner_df_wide$euthanasia.m.4
dat$x5 <- partner_df_wide$euthanasia.m.5
dat$x6 <- partner_df_wide$euthanasia.m.6
dat$x7 <- partner_df_wide$euthanasia.m.7
dat$x8 <- partner_df_wide$euthanasia.m.8
dat$x9 <- partner_df_wide$euthanasia.m.9
dat$x10 <- partner_df_wide$euthanasia.m.10
dat$x11 <- partner_df_wide$euthanasia.m.11
dat$y1 <- partner_df_wide$euthanasia.f.1
dat$y2 <- partner_df_wide$euthanasia.f.2
dat$y3 <- partner_df_wide$euthanasia.f.3
dat$y4 <- partner_df_wide$euthanasia.f.4
dat$y5 <- partner_df_wide$euthanasia.f.5
dat$y6 <- partner_df_wide$euthanasia.f.6
dat$y7 <- partner_df_wide$euthanasia.f.7
dat$y8 <- partner_df_wide$euthanasia.f.8
dat$y9 <- partner_df_wide$euthanasia.f.9
dat$y10 <- partner_df_wide$euthanasia.f.10
dat$y11 <- partner_df_wide$euthanasia.f.11
# treat education as a time stable. And use all available data.
dat$oplx <- rowMeans(partner_df_wide[, c("oplmet.m.1", "oplmet.m.2", "oplmet.m.3", "oplmet.m.4", "oplmet.m.5",
"oplmet.m.6", "oplmet.m.7", "oplmet.m.8", "oplmet.m.9", "oplmet.m.10", "oplmet.m.11")], na.rm = T)
dat$oply <- rowMeans(partner_df_wide[, c("oplmet.f.1", "oplmet.f.2", "oplmet.f.3", "oplmet.f.4", "oplmet.f.5",
"oplmet.f.6", "oplmet.f.7", "oplmet.f.8", "oplmet.f.9", "oplmet.f.10", "oplmet.f.11")], na.rm = T)
# calculate diff in education between men and women
dat$oplxy <- dat$oplx - dat$oply
# table(dat$oplx, dat$oply, useNA = 'always') hist(dat$oplxy)
# define three groups for multigroup analyses
dat$oplgroup <- ifelse(dat$oplxy > 1, "menhigher", NA)
dat$oplgroup <- ifelse(dat$oplxy < -1, "womenhigher", dat$oplgroup)
dat$oplgroup <- ifelse(dat$oplxy <= 1 & dat$oplxy >= -1, "equal", dat$oplgroup)
# table(dat$oplgroup, useNA = 'always')
dat_ori <- dat
datalist_ori[[3]] <- dat_ori
# dep4: income_diff
dat <- data.frame(x1 = partner_df_wide$income_diff.m.1)
dat$x2 <- partner_df_wide$income_diff.m.2
dat$x3 <- partner_df_wide$income_diff.m.3
dat$x4 <- partner_df_wide$income_diff.m.4
dat$x5 <- partner_df_wide$income_diff.m.5
dat$x6 <- partner_df_wide$income_diff.m.6
dat$x7 <- partner_df_wide$income_diff.m.7
dat$x8 <- partner_df_wide$income_diff.m.8
dat$x9 <- partner_df_wide$income_diff.m.9
dat$x10 <- partner_df_wide$income_diff.m.10
dat$x11 <- partner_df_wide$income_diff.m.11
dat$y1 <- partner_df_wide$income_diff.f.1
dat$y2 <- partner_df_wide$income_diff.f.2
dat$y3 <- partner_df_wide$income_diff.f.3
dat$y4 <- partner_df_wide$income_diff.f.4
dat$y5 <- partner_df_wide$income_diff.f.5
dat$y6 <- partner_df_wide$income_diff.f.6
dat$y7 <- partner_df_wide$income_diff.f.7
dat$y8 <- partner_df_wide$income_diff.f.8
dat$y9 <- partner_df_wide$income_diff.f.9
dat$y10 <- partner_df_wide$income_diff.f.10
dat$y11 <- partner_df_wide$income_diff.f.11
# treat education as a time stable. And use all available data.
dat$oplx <- rowMeans(partner_df_wide[, c("oplmet.m.1", "oplmet.m.2", "oplmet.m.3", "oplmet.m.4", "oplmet.m.5",
"oplmet.m.6", "oplmet.m.7", "oplmet.m.8", "oplmet.m.9", "oplmet.m.10", "oplmet.m.11")], na.rm = T)
dat$oply <- rowMeans(partner_df_wide[, c("oplmet.f.1", "oplmet.f.2", "oplmet.f.3", "oplmet.f.4", "oplmet.f.5",
"oplmet.f.6", "oplmet.f.7", "oplmet.f.8", "oplmet.f.9", "oplmet.f.10", "oplmet.f.11")], na.rm = T)
# calculate diff in education between men and women
dat$oplxy <- dat$oplx - dat$oply
# table(dat$oplx, dat$oply, useNA = 'always') hist(dat$oplxy)
# define three groups for multigroup analyses
dat$oplgroup <- ifelse(dat$oplxy > 1, "menhigher", NA)
dat$oplgroup <- ifelse(dat$oplxy < -1, "womenhigher", dat$oplgroup)
dat$oplgroup <- ifelse(dat$oplxy <= 1 & dat$oplxy >= -1, "equal", dat$oplgroup)
# table(dat$oplgroup, useNA = 'always')
dat_ori <- dat
datalist_ori[[4]] <- dat_ori3.6.2 Modelling strategy
takes into account that observations within couples are interdependent;
that can explain the interdependence at the couple level;
focus on changes taking place within couples, not on changes between couples;
clearly distinguishes between:
- Actor effects: stability effects
- Partner effects: influence effects
Is flexible, so we can control, for example, for educational effects. A model that tickes all the boxes is the Random Intercep Cross-Lagged Panel Model.
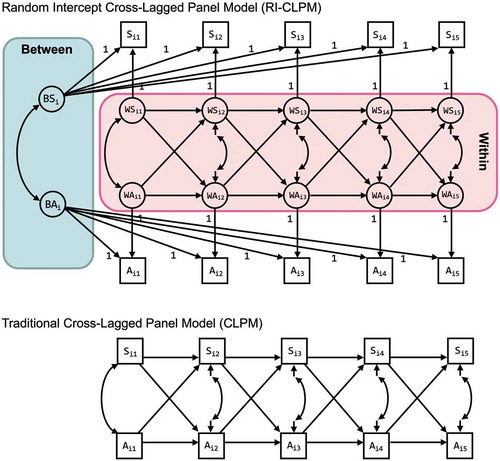
Figure 3.1: RI-CLPM
Source: (Mulder and Hamaker 2020)
3.6.3 Robustness
We will compare the results across four different modeling strategies:
- Cross-lagged Panel Model (CLPM) (11 waves). This model lumps together between couple effects and within couples effects but it may help us to compare results.
- RI-CLPM (11 waves). We will focus on this model!
- RI-CLPM + structural time trends (11 waves). This model takes into account that there may also be general period (or structural) trends in the opinions.
- RI/RS-CLPM (11 waves). Finally, in this model we take into account that spouses may show different (linear) trends in their opinions for reasons we do not know. It is a random-intercept, random-slope growth curve model for the two spouses combined.
We will test our hypotheses for four different dependent variables:
- eu-integration
- immigration
- euthanasia
- income differences
3.6.4 Results hypo1
Hypo1 RI-CLPM: When your partner’s opinion is relatively high (compared to your partners average opinion over time) at time T, your own opinion will be relatively high (compared to your own average opinion over time) at time T+1.
3.6.4.1 CLPM
results <- list()
myModel <- "
### control for education
x1 + x2 + x3 +x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 ~ e*oplx
y1 + y2 + y3 +y4 + y5 + y6 + y7 + y8 + y9 + y10 + y11 ~ e*oply
### Estimate the lagged effects
x2 ~ a*x1 + b*y1
x3 ~ a*x2 + b*y2
x4 ~ a*x3 + b*y3
x5 ~ a*x4 + b*y4
x6 ~ a*x5 + b*y5
x7 ~ a*x6 + b*y6
x8 ~ a*x7 + b*y7
x9 ~ a*x8 + b*y8
x10 ~ a*x9 + b*y9
x11 ~ a*x10 + b*y10
y2 ~ b*x1 + a*y1
y3 ~ b*x2 + a*y2
y4 ~ b*x3 + a*y3
y5 ~ b*x4 + a*y4
y6 ~ b*x5 + a*y5
y7 ~ b*x6 + a*y6
y8 ~ b*x7 + a*y7
y9 ~ b*x8 + a*y8
y10 ~ b*x9 + a*y9
y11 ~ b*x10 + a*y10
# Estimate the (residual) covariance between the variables
x1 ~~ y1 # Covariance
x2 ~~ y2
x3 ~~ y3
x4 ~~ y4
x5 ~~ y5
x6 ~~ y6
x7 ~~ y7
x8 ~~ y8
x9 ~~ y9
x10 ~~ y10
x11 ~~ y11
# Estimate the (residual) variance of the variables.
x1 ~~ x1 # Variances
y1 ~~ y1
x2 ~~ x2 # Residual variances
y2 ~~ y2
x3 ~~ x3
y3 ~~ y3
x4 ~~ x4
y4 ~~ y4
x5 ~~ x5
y5 ~~ y5
x6 ~~ x6
y6 ~~ y6
x7 ~~ x7
y7 ~~ y7
x8 ~~ x8
y8 ~~ y8
x9 ~~ x9
y9 ~~ y9
x10 ~~ x10
y10 ~~ y10
x11 ~~ x11
y11 ~~ y11
#intercepts
x1 ~ 1
y1 ~ 1
x2 ~ 1
y2 ~ 1
x3 ~ 1
y3 ~ 1
x4 ~ 1
y4 ~ 1
x5 ~ 1
y5 ~ 1
x6 ~ 1
y6 ~ 1
x7 ~ 1
y7 ~ 1
x8 ~ 1
y8 ~ 1
x9 ~ 1
y9 ~ 1
x10 ~ 1
y10 ~ 1
x11 ~ 1
y11 ~ 1
"
# Estimate models a bit faster:
estimate <- function(x) lavaan(myModel, data = x, missing = "fiml.x", meanstructure = T)
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
results[[1]] <- results_temp[[1]]
results[[2]] <- results_temp[[2]]
results[[3]] <- results_temp[[3]]
results[[4]] <- results_temp[[4]]
names(results)[1:4] <- c("fitm1h1y1", "fitm1h1y2", "fitm1h1y3", "fitm1h1y4")
save(results, file = "results.RData")load("addfiles/results.Rdata")
summary(results[[1]])
summary(results[[2]])
summary(results[[3]])
summary(results[[4]])#> lavaan 0.6-11 ended normally after 31 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 59
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 3353.035
#> Degrees of freedom 261
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x2 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x3 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x4 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x5 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x6 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x7 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x8 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x9 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x10 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> x11 ~
#> oplx (e) 0.039 0.002 22.760 0.000
#> y1 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y2 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y3 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y4 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y5 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y6 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y7 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y8 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y9 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y10 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> y11 ~
#> oply (e) 0.039 0.002 22.760 0.000
#> x2 ~
#> x1 (a) 0.572 0.005 114.096 0.000
#> y1 (b) 0.150 0.005 29.318 0.000
#> x3 ~
#> x2 (a) 0.572 0.005 114.096 0.000
#> y2 (b) 0.150 0.005 29.318 0.000
#> x4 ~
#> x3 (a) 0.572 0.005 114.096 0.000
#> y3 (b) 0.150 0.005 29.318 0.000
#> x5 ~
#> x4 (a) 0.572 0.005 114.096 0.000
#> y4 (b) 0.150 0.005 29.318 0.000
#> x6 ~
#> x5 (a) 0.572 0.005 114.096 0.000
#> y5 (b) 0.150 0.005 29.318 0.000
#> x7 ~
#> x6 (a) 0.572 0.005 114.096 0.000
#> y6 (b) 0.150 0.005 29.318 0.000
#> x8 ~
#> x7 (a) 0.572 0.005 114.096 0.000
#> y7 (b) 0.150 0.005 29.318 0.000
#> x9 ~
#> x8 (a) 0.572 0.005 114.096 0.000
#> y8 (b) 0.150 0.005 29.318 0.000
#> x10 ~
#> x9 (a) 0.572 0.005 114.096 0.000
#> y9 (b) 0.150 0.005 29.318 0.000
#> x11 ~
#> x10 (a) 0.572 0.005 114.096 0.000
#> y10 (b) 0.150 0.005 29.318 0.000
#> y2 ~
#> x1 (b) 0.150 0.005 29.318 0.000
#> y1 (a) 0.572 0.005 114.096 0.000
#> y3 ~
#> x2 (b) 0.150 0.005 29.318 0.000
#> y2 (a) 0.572 0.005 114.096 0.000
#> y4 ~
#> x3 (b) 0.150 0.005 29.318 0.000
#> y3 (a) 0.572 0.005 114.096 0.000
#> y5 ~
#> x4 (b) 0.150 0.005 29.318 0.000
#> y4 (a) 0.572 0.005 114.096 0.000
#> y6 ~
#> x5 (b) 0.150 0.005 29.318 0.000
#> y5 (a) 0.572 0.005 114.096 0.000
#> y7 ~
#> x6 (b) 0.150 0.005 29.318 0.000
#> y6 (a) 0.572 0.005 114.096 0.000
#> y8 ~
#> x7 (b) 0.150 0.005 29.318 0.000
#> y7 (a) 0.572 0.005 114.096 0.000
#> y9 ~
#> x8 (b) 0.150 0.005 29.318 0.000
#> y8 (a) 0.572 0.005 114.096 0.000
#> y10 ~
#> x9 (b) 0.150 0.005 29.318 0.000
#> y9 (a) 0.572 0.005 114.096 0.000
#> y11 ~
#> x10 (b) 0.150 0.005 29.318 0.000
#> y10 (a) 0.572 0.005 114.096 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.410 0.030 13.695 0.000
#> .x2 ~~
#> .y2 0.121 0.021 5.706 0.000
#> .x3 ~~
#> .y3 0.118 0.020 5.806 0.000
#> .x4 ~~
#> .y4 0.152 0.022 7.063 0.000
#> .x5 ~~
#> .y5 0.147 0.025 5.937 0.000
#> .x6 ~~
#> .y6 0.110 0.020 5.561 0.000
#> .x7 ~~
#> .y7 0.105 0.018 5.991 0.000
#> .x8 ~~
#> .y8 0.112 0.021 5.242 0.000
#> .x9 ~~
#> .y9 0.119 0.022 5.444 0.000
#> .x10 ~~
#> .y10 0.078 0.023 3.335 0.001
#> .x11 ~~
#> .y11 0.130 0.024 5.493 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.133 0.034 33.382 0.000
#> .y1 1.087 0.031 35.251 0.000
#> .x2 0.089 0.031 2.898 0.004
#> .y2 0.072 0.029 2.469 0.014
#> .x3 0.016 0.031 0.509 0.611
#> .y3 0.007 0.028 0.245 0.806
#> .x4 -0.285 0.031 -9.066 0.000
#> .y4 -0.326 0.029 -11.062 0.000
#> .x5 0.107 0.032 3.285 0.001
#> .y5 -0.082 0.030 -2.748 0.006
#> .x6 -0.190 0.030 -6.311 0.000
#> .y6 -0.150 0.029 -5.257 0.000
#> .x7 -0.187 0.029 -6.370 0.000
#> .y7 -0.185 0.028 -6.666 0.000
#> .x8 -0.017 0.031 -0.564 0.573
#> .y8 -0.032 0.029 -1.094 0.274
#> .x9 -0.169 0.031 -5.452 0.000
#> .y9 -0.112 0.030 -3.758 0.000
#> .x10 0.041 0.032 1.282 0.200
#> .y10 0.077 0.031 2.492 0.013
#> .x11 0.033 0.033 0.992 0.321
#> .y11 0.029 0.031 0.948 0.343
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.384 0.046 30.338 0.000
#> .y1 1.007 0.034 29.508 0.000
#> .x2 0.824 0.031 27.005 0.000
#> .y2 0.685 0.026 26.343 0.000
#> .x3 0.781 0.030 26.387 0.000
#> .y3 0.595 0.023 25.454 0.000
#> .x4 0.814 0.032 25.716 0.000
#> .y4 0.639 0.026 25.011 0.000
#> .x5 0.945 0.037 25.737 0.000
#> .y5 0.694 0.028 25.003 0.000
#> .x6 0.709 0.027 25.842 0.000
#> .y6 0.581 0.023 24.975 0.000
#> .x7 0.646 0.025 25.635 0.000
#> .y7 0.523 0.021 25.036 0.000
#> .x8 0.754 0.030 25.271 0.000
#> .y8 0.626 0.025 24.953 0.000
#> .x9 0.753 0.029 25.582 0.000
#> .y9 0.646 0.026 24.747 0.000
#> .x10 0.766 0.032 24.282 0.000
#> .y10 0.651 0.028 23.475 0.000
#> .x11 0.796 0.033 24.016 0.000
#> .y11 0.620 0.027 22.840 0.000
#>
#> lavaan 0.6-11 ended normally after 26 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 59
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 4312.762
#> Degrees of freedom 261
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x2 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x3 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x4 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x5 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x6 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x7 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x8 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x9 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x10 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> x11 ~
#> oplx (e) 0.026 0.001 18.920 0.000
#> y1 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y2 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y3 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y4 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y5 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y6 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y7 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y8 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y9 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y10 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> y11 ~
#> oply (e) 0.026 0.001 18.920 0.000
#> x2 ~
#> x1 (a) 0.570 0.005 117.122 0.000
#> y1 (b) 0.164 0.005 32.553 0.000
#> x3 ~
#> x2 (a) 0.570 0.005 117.122 0.000
#> y2 (b) 0.164 0.005 32.553 0.000
#> x4 ~
#> x3 (a) 0.570 0.005 117.122 0.000
#> y3 (b) 0.164 0.005 32.553 0.000
#> x5 ~
#> x4 (a) 0.570 0.005 117.122 0.000
#> y4 (b) 0.164 0.005 32.553 0.000
#> x6 ~
#> x5 (a) 0.570 0.005 117.122 0.000
#> y5 (b) 0.164 0.005 32.553 0.000
#> x7 ~
#> x6 (a) 0.570 0.005 117.122 0.000
#> y6 (b) 0.164 0.005 32.553 0.000
#> x8 ~
#> x7 (a) 0.570 0.005 117.122 0.000
#> y7 (b) 0.164 0.005 32.553 0.000
#> x9 ~
#> x8 (a) 0.570 0.005 117.122 0.000
#> y8 (b) 0.164 0.005 32.553 0.000
#> x10 ~
#> x9 (a) 0.570 0.005 117.122 0.000
#> y9 (b) 0.164 0.005 32.553 0.000
#> x11 ~
#> x10 (a) 0.570 0.005 117.122 0.000
#> y10 (b) 0.164 0.005 32.553 0.000
#> y2 ~
#> x1 (b) 0.164 0.005 32.553 0.000
#> y1 (a) 0.570 0.005 117.122 0.000
#> y3 ~
#> x2 (b) 0.164 0.005 32.553 0.000
#> y2 (a) 0.570 0.005 117.122 0.000
#> y4 ~
#> x3 (b) 0.164 0.005 32.553 0.000
#> y3 (a) 0.570 0.005 117.122 0.000
#> y5 ~
#> x4 (b) 0.164 0.005 32.553 0.000
#> y4 (a) 0.570 0.005 117.122 0.000
#> y6 ~
#> x5 (b) 0.164 0.005 32.553 0.000
#> y5 (a) 0.570 0.005 117.122 0.000
#> y7 ~
#> x6 (b) 0.164 0.005 32.553 0.000
#> y6 (a) 0.570 0.005 117.122 0.000
#> y8 ~
#> x7 (b) 0.164 0.005 32.553 0.000
#> y7 (a) 0.570 0.005 117.122 0.000
#> y9 ~
#> x8 (b) 0.164 0.005 32.553 0.000
#> y8 (a) 0.570 0.005 117.122 0.000
#> y10 ~
#> x9 (b) 0.164 0.005 32.553 0.000
#> y9 (a) 0.570 0.005 117.122 0.000
#> y11 ~
#> x10 (b) 0.164 0.005 32.553 0.000
#> y10 (a) 0.570 0.005 117.122 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.383 0.023 16.619 0.000
#> .x2 ~~
#> .y2 0.101 0.015 6.622 0.000
#> .x3 ~~
#> .y3 0.104 0.015 6.806 0.000
#> .x4 ~~
#> .y4 0.071 0.014 5.067 0.000
#> .x5 ~~
#> .y5 0.086 0.014 6.103 0.000
#> .x6 ~~
#> .y6 0.074 0.014 5.391 0.000
#> .x7 ~~
#> .y7 0.055 0.014 4.035 0.000
#> .x8 ~~
#> .y8 0.075 0.015 5.121 0.000
#> .x9 ~~
#> .y9 0.040 0.015 2.684 0.007
#> .x10 ~~
#> .y10 0.089 0.015 5.887 0.000
#> .x11 ~~
#> .y11 0.102 0.015 6.774 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.892 0.028 32.245 0.000
#> .y1 0.953 0.027 35.963 0.000
#> .x2 0.026 0.025 1.038 0.299
#> .y2 0.057 0.024 2.331 0.020
#> .x3 -0.002 0.025 -0.089 0.929
#> .y3 0.068 0.024 2.803 0.005
#> .x4 -0.001 0.024 -0.058 0.953
#> .y4 0.039 0.024 1.593 0.111
#> .x5 -0.003 0.025 -0.140 0.888
#> .y5 0.039 0.024 1.599 0.110
#> .x6 -0.005 0.025 -0.192 0.848
#> .y6 0.039 0.024 1.656 0.098
#> .x7 0.018 0.025 0.708 0.479
#> .y7 0.065 0.024 2.701 0.007
#> .x8 -0.048 0.025 -1.921 0.055
#> .y8 0.002 0.025 0.097 0.923
#> .x9 -0.058 0.025 -2.280 0.023
#> .y9 0.018 0.025 0.725 0.468
#> .x10 0.103 0.026 3.933 0.000
#> .y10 0.127 0.025 5.052 0.000
#> .x11 -0.011 0.026 -0.420 0.675
#> .y11 0.053 0.026 2.085 0.037
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.945 0.031 30.290 0.000
#> .y1 0.870 0.029 30.158 0.000
#> .x2 0.567 0.021 27.155 0.000
#> .y2 0.551 0.020 27.179 0.000
#> .x3 0.548 0.021 26.526 0.000
#> .y3 0.504 0.019 26.218 0.000
#> .x4 0.462 0.018 25.877 0.000
#> .y4 0.485 0.019 25.485 0.000
#> .x5 0.478 0.019 25.817 0.000
#> .y5 0.462 0.018 25.165 0.000
#> .x6 0.506 0.019 26.234 0.000
#> .y6 0.442 0.017 26.326 0.000
#> .x7 0.489 0.019 25.936 0.000
#> .y7 0.450 0.017 26.082 0.000
#> .x8 0.479 0.019 25.456 0.000
#> .y8 0.483 0.019 25.545 0.000
#> .x9 0.502 0.019 25.775 0.000
#> .y9 0.506 0.020 25.464 0.000
#> .x10 0.512 0.021 24.658 0.000
#> .y10 0.454 0.019 24.272 0.000
#> .x11 0.492 0.020 24.435 0.000
#> .y11 0.451 0.019 24.036 0.000
#>
#> lavaan 0.6-11 ended normally after 74 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 59
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5151.101
#> Degrees of freedom 261
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x2 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x3 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x4 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x5 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x6 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x7 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x8 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x9 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x10 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> x11 ~
#> oplx (e) 0.004 0.001 3.326 0.001
#> y1 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y2 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y3 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y4 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y5 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y6 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y7 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y8 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y9 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y10 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> y11 ~
#> oply (e) 0.004 0.001 3.326 0.001
#> x2 ~
#> x1 (a) 0.680 0.004 158.832 0.000
#> y1 (b) 0.182 0.004 41.580 0.000
#> x3 ~
#> x2 (a) 0.680 0.004 158.832 0.000
#> y2 (b) 0.182 0.004 41.580 0.000
#> x4 ~
#> x3 (a) 0.680 0.004 158.832 0.000
#> y3 (b) 0.182 0.004 41.580 0.000
#> x5 ~
#> x4 (a) 0.680 0.004 158.832 0.000
#> y4 (b) 0.182 0.004 41.580 0.000
#> x6 ~
#> x5 (a) 0.680 0.004 158.832 0.000
#> y5 (b) 0.182 0.004 41.580 0.000
#> x7 ~
#> x6 (a) 0.680 0.004 158.832 0.000
#> y6 (b) 0.182 0.004 41.580 0.000
#> x8 ~
#> x7 (a) 0.680 0.004 158.832 0.000
#> y7 (b) 0.182 0.004 41.580 0.000
#> x9 ~
#> x8 (a) 0.680 0.004 158.832 0.000
#> y8 (b) 0.182 0.004 41.580 0.000
#> x10 ~
#> x9 (a) 0.680 0.004 158.832 0.000
#> y9 (b) 0.182 0.004 41.580 0.000
#> x11 ~
#> x10 (a) 0.680 0.004 158.832 0.000
#> y10 (b) 0.182 0.004 41.580 0.000
#> y2 ~
#> x1 (b) 0.182 0.004 41.580 0.000
#> y1 (a) 0.680 0.004 158.832 0.000
#> y3 ~
#> x2 (b) 0.182 0.004 41.580 0.000
#> y2 (a) 0.680 0.004 158.832 0.000
#> y4 ~
#> x3 (b) 0.182 0.004 41.580 0.000
#> y3 (a) 0.680 0.004 158.832 0.000
#> y5 ~
#> x4 (b) 0.182 0.004 41.580 0.000
#> y4 (a) 0.680 0.004 158.832 0.000
#> y6 ~
#> x5 (b) 0.182 0.004 41.580 0.000
#> y5 (a) 0.680 0.004 158.832 0.000
#> y7 ~
#> x6 (b) 0.182 0.004 41.580 0.000
#> y6 (a) 0.680 0.004 158.832 0.000
#> y8 ~
#> x7 (b) 0.182 0.004 41.580 0.000
#> y7 (a) 0.680 0.004 158.832 0.000
#> y9 ~
#> x8 (b) 0.182 0.004 41.580 0.000
#> y8 (a) 0.680 0.004 158.832 0.000
#> y10 ~
#> x9 (b) 0.182 0.004 41.580 0.000
#> y9 (a) 0.680 0.004 158.832 0.000
#> y11 ~
#> x10 (b) 0.182 0.004 41.580 0.000
#> y10 (a) 0.680 0.004 158.832 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.658 0.029 22.943 0.000
#> .x2 ~~
#> .y2 0.081 0.012 6.912 0.000
#> .x3 ~~
#> .y3 0.086 0.011 7.800 0.000
#> .x4 ~~
#> .y4 0.086 0.011 7.867 0.000
#> .x5 ~~
#> .y5 0.077 0.010 7.447 0.000
#> .x6 ~~
#> .y6 0.066 0.009 7.440 0.000
#> .x7 ~~
#> .y7 0.057 0.009 6.176 0.000
#> .x8 ~~
#> .y8 0.063 0.010 6.072 0.000
#> .x9 ~~
#> .y9 0.074 0.010 7.093 0.000
#> .x10 ~~
#> .y10 0.096 0.013 7.554 0.000
#> .x11 ~~
#> .y11 0.101 0.012 8.407 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 4.256 0.026 161.422 0.000
#> .y1 4.274 0.026 161.379 0.000
#> .x2 0.559 0.027 20.780 0.000
#> .y2 0.587 0.026 22.511 0.000
#> .x3 0.537 0.026 20.488 0.000
#> .y3 0.529 0.027 19.968 0.000
#> .x4 0.579 0.026 22.213 0.000
#> .y4 0.601 0.027 22.523 0.000
#> .x5 0.567 0.026 21.500 0.000
#> .y5 0.581 0.026 22.174 0.000
#> .x6 0.569 0.026 21.651 0.000
#> .y6 0.572 0.025 22.816 0.000
#> .x7 0.587 0.026 22.663 0.000
#> .y7 0.587 0.026 22.866 0.000
#> .x8 0.570 0.026 21.537 0.000
#> .y8 0.575 0.027 21.666 0.000
#> .x9 0.509 0.027 18.825 0.000
#> .y9 0.535 0.026 20.449 0.000
#> .x10 0.543 0.028 19.517 0.000
#> .y10 0.544 0.027 20.026 0.000
#> .x11 0.597 0.028 21.710 0.000
#> .y11 0.600 0.027 21.817 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.060 0.034 31.095 0.000
#> .y1 1.113 0.036 30.875 0.000
#> .x2 0.440 0.016 26.862 0.000
#> .y2 0.392 0.015 26.637 0.000
#> .x3 0.359 0.014 26.181 0.000
#> .y3 0.408 0.016 25.925 0.000
#> .x4 0.338 0.013 26.091 0.000
#> .y4 0.403 0.016 25.781 0.000
#> .x5 0.339 0.013 25.647 0.000
#> .y5 0.347 0.014 25.241 0.000
#> .x6 0.344 0.013 26.462 0.000
#> .y6 0.272 0.011 25.709 0.000
#> .x7 0.308 0.012 25.948 0.000
#> .y7 0.308 0.012 25.196 0.000
#> .x8 0.325 0.013 25.093 0.000
#> .y8 0.351 0.014 24.731 0.000
#> .x9 0.367 0.015 25.327 0.000
#> .y9 0.321 0.013 25.158 0.000
#> .x10 0.394 0.017 23.697 0.000
#> .y10 0.360 0.015 23.902 0.000
#> .x11 0.362 0.015 24.067 0.000
#> .y11 0.367 0.015 23.792 0.000
#>
#> lavaan 0.6-11 ended normally after 48 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 59
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 4211.139
#> Degrees of freedom 261
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x2 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x3 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x4 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x5 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x6 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x7 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x8 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x9 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x10 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> x11 ~
#> oplx (e) -0.017 0.001 -11.913 0.000
#> y1 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y2 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y3 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y4 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y5 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y6 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y7 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y8 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y9 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y10 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> y11 ~
#> oply (e) -0.017 0.001 -11.913 0.000
#> x2 ~
#> x1 (a) 0.576 0.005 117.622 0.000
#> y1 (b) 0.146 0.005 28.545 0.000
#> x3 ~
#> x2 (a) 0.576 0.005 117.622 0.000
#> y2 (b) 0.146 0.005 28.545 0.000
#> x4 ~
#> x3 (a) 0.576 0.005 117.622 0.000
#> y3 (b) 0.146 0.005 28.545 0.000
#> x5 ~
#> x4 (a) 0.576 0.005 117.622 0.000
#> y4 (b) 0.146 0.005 28.545 0.000
#> x6 ~
#> x5 (a) 0.576 0.005 117.622 0.000
#> y5 (b) 0.146 0.005 28.545 0.000
#> x7 ~
#> x6 (a) 0.576 0.005 117.622 0.000
#> y6 (b) 0.146 0.005 28.545 0.000
#> x8 ~
#> x7 (a) 0.576 0.005 117.622 0.000
#> y7 (b) 0.146 0.005 28.545 0.000
#> x9 ~
#> x8 (a) 0.576 0.005 117.622 0.000
#> y8 (b) 0.146 0.005 28.545 0.000
#> x10 ~
#> x9 (a) 0.576 0.005 117.622 0.000
#> y9 (b) 0.146 0.005 28.545 0.000
#> x11 ~
#> x10 (a) 0.576 0.005 117.622 0.000
#> y10 (b) 0.146 0.005 28.545 0.000
#> y2 ~
#> x1 (b) 0.146 0.005 28.545 0.000
#> y1 (a) 0.576 0.005 117.622 0.000
#> y3 ~
#> x2 (b) 0.146 0.005 28.545 0.000
#> y2 (a) 0.576 0.005 117.622 0.000
#> y4 ~
#> x3 (b) 0.146 0.005 28.545 0.000
#> y3 (a) 0.576 0.005 117.622 0.000
#> y5 ~
#> x4 (b) 0.146 0.005 28.545 0.000
#> y4 (a) 0.576 0.005 117.622 0.000
#> y6 ~
#> x5 (b) 0.146 0.005 28.545 0.000
#> y5 (a) 0.576 0.005 117.622 0.000
#> y7 ~
#> x6 (b) 0.146 0.005 28.545 0.000
#> y6 (a) 0.576 0.005 117.622 0.000
#> y8 ~
#> x7 (b) 0.146 0.005 28.545 0.000
#> y7 (a) 0.576 0.005 117.622 0.000
#> y9 ~
#> x8 (b) 0.146 0.005 28.545 0.000
#> y8 (a) 0.576 0.005 117.622 0.000
#> y10 ~
#> x9 (b) 0.146 0.005 28.545 0.000
#> y9 (a) 0.576 0.005 117.622 0.000
#> y11 ~
#> x10 (b) 0.146 0.005 28.545 0.000
#> y10 (a) 0.576 0.005 117.622 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.421 0.025 16.651 0.000
#> .x2 ~~
#> .y2 0.140 0.016 8.804 0.000
#> .x3 ~~
#> .y3 0.099 0.016 6.283 0.000
#> .x4 ~~
#> .y4 0.110 0.017 6.538 0.000
#> .x5 ~~
#> .y5 0.062 0.014 4.389 0.000
#> .x6 ~~
#> .y6 0.132 0.016 8.277 0.000
#> .x7 ~~
#> .y7 0.092 0.014 6.442 0.000
#> .x8 ~~
#> .y8 0.084 0.016 5.379 0.000
#> .x9 ~~
#> .y9 0.103 0.017 6.144 0.000
#> .x10 ~~
#> .y10 0.094 0.017 5.492 0.000
#> .x11 ~~
#> .y11 0.069 0.017 3.957 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 3.856 0.029 130.976 0.000
#> .y1 4.007 0.027 146.050 0.000
#> .x2 1.238 0.035 35.035 0.000
#> .y2 1.350 0.034 39.374 0.000
#> .x3 1.210 0.035 34.432 0.000
#> .y3 1.249 0.035 35.770 0.000
#> .x4 1.210 0.036 34.057 0.000
#> .y4 1.294 0.035 37.093 0.000
#> .x5 1.328 0.035 38.257 0.000
#> .y5 1.345 0.034 39.097 0.000
#> .x6 1.135 0.036 31.683 0.000
#> .y6 1.215 0.035 34.565 0.000
#> .x7 1.227 0.035 35.149 0.000
#> .y7 1.269 0.034 37.270 0.000
#> .x8 1.276 0.036 35.898 0.000
#> .y8 1.323 0.035 37.776 0.000
#> .x9 1.262 0.036 35.163 0.000
#> .y9 1.286 0.036 36.048 0.000
#> .x10 1.252 0.036 34.580 0.000
#> .y10 1.253 0.036 34.746 0.000
#> .x11 1.303 0.037 35.598 0.000
#> .y11 1.283 0.036 35.215 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.095 0.036 30.386 0.000
#> .y1 0.910 0.030 30.280 0.000
#> .x2 0.608 0.022 27.022 0.000
#> .y2 0.541 0.020 27.090 0.000
#> .x3 0.541 0.021 26.339 0.000
#> .y3 0.555 0.021 26.223 0.000
#> .x4 0.565 0.022 25.748 0.000
#> .y4 0.532 0.021 25.544 0.000
#> .x5 0.468 0.018 25.316 0.000
#> .y5 0.471 0.019 25.266 0.000
#> .x6 0.562 0.021 26.194 0.000
#> .y6 0.532 0.020 26.158 0.000
#> .x7 0.502 0.019 25.972 0.000
#> .y7 0.444 0.017 25.676 0.000
#> .x8 0.535 0.021 25.603 0.000
#> .y8 0.505 0.020 25.362 0.000
#> .x9 0.552 0.021 25.758 0.000
#> .y9 0.542 0.021 25.218 0.000
#> .x10 0.532 0.022 24.556 0.000
#> .y10 0.531 0.022 24.152 0.000
#> .x11 0.543 0.022 24.310 0.000
#> .y11 0.525 0.022 23.738 0.0003.6.4.2 RI-CLPM
RICLPM <- '
# Create between components (random intercepts)
RIx =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11
RIy =~ 1*y1 + 1*y2 + 1*y3 + 1*y4 + 1*y5 + 1*y6 + 1*y7 + 1*y8 + 1*y9 + 1*y10 + 1*y11
RIx ~ e*oplx
RIy ~ e*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
wx2 ~ a*wx1 + b*wy1
wx3 ~ a*wx2 + b*wy2
wx4 ~ a*wx3 + b*wy3
wx5 ~ a*wx4 + b*wy4
wx6 ~ a*wx5 + b*wy5
wx7 ~ a*wx6 + b*wy6
wx8 ~ a*wx7 + b*wy7
wx9 ~ a*wx8 + b*wy8
wx10 ~ a*wx9 + b*wy9
wx11 ~ a*wx10 + b*wy10
wy2 ~ b*wx1 + a*wy1
wy3 ~ b*wx2 + a*wy2
wy4 ~ b*wx3 + a*wy3
wy5 ~ b*wx4 + a*wy4
wy6 ~ b*wx5 + a*wy5
wy7 ~ b*wx6 + a*wy6
wy8 ~ b*wx7 + a*wy7
wy9 ~ b*wx8 + a*wy8
wy10 ~ b*wx9 + a*wy9
wy11 ~ b*wx10 + a*wy10
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(RICLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
results[[5]] <- results_temp[[1]]
results[[6]] <- results_temp[[2]]
results[[7]] <- results_temp[[3]]
results[[8]] <- results_temp[[4]]
names(results)[5:8] <- c("fitm2h1y1", "fitm2h1y2","fitm2h1y3","fitm2h1y4")load("addfiles/results.Rdata")
summary(results[[5]])
summary(results[[6]])
summary(results[[7]])
summary(results[[8]])#> lavaan 0.6-11 ended normally after 42 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1632.289
#> Degrees of freedom 280
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.122 0.001 107.040 0.000
#> RIy ~
#> oply (e) 0.122 0.001 107.040 0.000
#> wx2 ~
#> wx1 (a) 0.203 0.008 24.374 0.000
#> wy1 (b) 0.075 0.009 8.629 0.000
#> wx3 ~
#> wx2 (a) 0.203 0.008 24.374 0.000
#> wy2 (b) 0.075 0.009 8.629 0.000
#> wx4 ~
#> wx3 (a) 0.203 0.008 24.374 0.000
#> wy3 (b) 0.075 0.009 8.629 0.000
#> wx5 ~
#> wx4 (a) 0.203 0.008 24.374 0.000
#> wy4 (b) 0.075 0.009 8.629 0.000
#> wx6 ~
#> wx5 (a) 0.203 0.008 24.374 0.000
#> wy5 (b) 0.075 0.009 8.629 0.000
#> wx7 ~
#> wx6 (a) 0.203 0.008 24.374 0.000
#> wy6 (b) 0.075 0.009 8.629 0.000
#> wx8 ~
#> wx7 (a) 0.203 0.008 24.374 0.000
#> wy7 (b) 0.075 0.009 8.629 0.000
#> wx9 ~
#> wx8 (a) 0.203 0.008 24.374 0.000
#> wy8 (b) 0.075 0.009 8.629 0.000
#> wx10 ~
#> wx9 (a) 0.203 0.008 24.374 0.000
#> wy9 (b) 0.075 0.009 8.629 0.000
#> wx11 ~
#> wx10 (a) 0.203 0.008 24.374 0.000
#> wy10 (b) 0.075 0.009 8.629 0.000
#> wy2 ~
#> wx1 (b) 0.075 0.009 8.629 0.000
#> wy1 (a) 0.203 0.008 24.374 0.000
#> wy3 ~
#> wx2 (b) 0.075 0.009 8.629 0.000
#> wy2 (a) 0.203 0.008 24.374 0.000
#> wy4 ~
#> wx3 (b) 0.075 0.009 8.629 0.000
#> wy3 (a) 0.203 0.008 24.374 0.000
#> wy5 ~
#> wx4 (b) 0.075 0.009 8.629 0.000
#> wy4 (a) 0.203 0.008 24.374 0.000
#> wy6 ~
#> wx5 (b) 0.075 0.009 8.629 0.000
#> wy5 (a) 0.203 0.008 24.374 0.000
#> wy7 ~
#> wx6 (b) 0.075 0.009 8.629 0.000
#> wy6 (a) 0.203 0.008 24.374 0.000
#> wy8 ~
#> wx7 (b) 0.075 0.009 8.629 0.000
#> wy7 (a) 0.203 0.008 24.374 0.000
#> wy9 ~
#> wx8 (b) 0.075 0.009 8.629 0.000
#> wy8 (a) 0.203 0.008 24.374 0.000
#> wy10 ~
#> wx9 (b) 0.075 0.009 8.629 0.000
#> wy9 (a) 0.203 0.008 24.374 0.000
#> wy11 ~
#> wx10 (b) 0.075 0.009 8.629 0.000
#> wy10 (a) 0.203 0.008 24.374 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.120 0.022 5.386 0.000
#> .wx2 ~~
#> .wy2 0.118 0.020 5.771 0.000
#> .wx3 ~~
#> .wy3 0.121 0.019 6.356 0.000
#> .wx4 ~~
#> .wy4 0.115 0.019 6.072 0.000
#> .wx5 ~~
#> .wy5 0.104 0.022 4.757 0.000
#> .wx6 ~~
#> .wy6 0.073 0.017 4.381 0.000
#> .wx7 ~~
#> .wy7 0.100 0.016 6.324 0.000
#> .wx8 ~~
#> .wy8 0.083 0.018 4.541 0.000
#> .wx9 ~~
#> .wy9 0.102 0.019 5.241 0.000
#> .wx10 ~~
#> .wy10 0.043 0.020 2.127 0.033
#> .wx11 ~~
#> .wy11 0.101 0.021 4.850 0.000
#> .RIx ~~
#> .RIy 0.354 0.017 21.005 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.757 0.025 30.317 0.000
#> .RIy 0.488 0.018 27.518 0.000
#> wx1 0.717 0.031 22.848 0.000
#> wy1 0.618 0.027 22.504 0.000
#> .wx2 0.712 0.029 24.248 0.000
#> .wy2 0.588 0.025 23.509 0.000
#> .wx3 0.614 0.026 23.815 0.000
#> .wy3 0.533 0.023 23.030 0.000
#> .wx4 0.604 0.027 22.679 0.000
#> .wy4 0.490 0.022 21.934 0.000
#> .wx5 0.758 0.032 24.016 0.000
#> .wy5 0.567 0.024 23.286 0.000
#> .wx6 0.510 0.022 22.955 0.000
#> .wy6 0.432 0.019 22.186 0.000
#> .wx7 0.488 0.021 22.844 0.000
#> .wy7 0.444 0.020 22.585 0.000
#> .wx8 0.546 0.024 23.023 0.000
#> .wy8 0.505 0.022 22.795 0.000
#> .wx9 0.604 0.026 23.063 0.000
#> .wy9 0.510 0.023 22.176 0.000
#> .wx10 0.562 0.026 21.674 0.000
#> .wy10 0.511 0.024 21.292 0.000
#> .wx11 0.612 0.028 21.517 0.000
#> .wy11 0.519 0.025 20.641 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 39 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 833.630
#> Degrees of freedom 280
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.104 0.001 103.001 0.000
#> RIy ~
#> oply (e) 0.104 0.001 103.001 0.000
#> wx2 ~
#> wx1 (a) 0.102 0.008 12.802 0.000
#> wy1 (b) 0.030 0.008 3.548 0.000
#> wx3 ~
#> wx2 (a) 0.102 0.008 12.802 0.000
#> wy2 (b) 0.030 0.008 3.548 0.000
#> wx4 ~
#> wx3 (a) 0.102 0.008 12.802 0.000
#> wy3 (b) 0.030 0.008 3.548 0.000
#> wx5 ~
#> wx4 (a) 0.102 0.008 12.802 0.000
#> wy4 (b) 0.030 0.008 3.548 0.000
#> wx6 ~
#> wx5 (a) 0.102 0.008 12.802 0.000
#> wy5 (b) 0.030 0.008 3.548 0.000
#> wx7 ~
#> wx6 (a) 0.102 0.008 12.802 0.000
#> wy6 (b) 0.030 0.008 3.548 0.000
#> wx8 ~
#> wx7 (a) 0.102 0.008 12.802 0.000
#> wy7 (b) 0.030 0.008 3.548 0.000
#> wx9 ~
#> wx8 (a) 0.102 0.008 12.802 0.000
#> wy8 (b) 0.030 0.008 3.548 0.000
#> wx10 ~
#> wx9 (a) 0.102 0.008 12.802 0.000
#> wy9 (b) 0.030 0.008 3.548 0.000
#> wx11 ~
#> wx10 (a) 0.102 0.008 12.802 0.000
#> wy10 (b) 0.030 0.008 3.548 0.000
#> wy2 ~
#> wx1 (b) 0.030 0.008 3.548 0.000
#> wy1 (a) 0.102 0.008 12.802 0.000
#> wy3 ~
#> wx2 (b) 0.030 0.008 3.548 0.000
#> wy2 (a) 0.102 0.008 12.802 0.000
#> wy4 ~
#> wx3 (b) 0.030 0.008 3.548 0.000
#> wy3 (a) 0.102 0.008 12.802 0.000
#> wy5 ~
#> wx4 (b) 0.030 0.008 3.548 0.000
#> wy4 (a) 0.102 0.008 12.802 0.000
#> wy6 ~
#> wx5 (b) 0.030 0.008 3.548 0.000
#> wy5 (a) 0.102 0.008 12.802 0.000
#> wy7 ~
#> wx6 (b) 0.030 0.008 3.548 0.000
#> wy6 (a) 0.102 0.008 12.802 0.000
#> wy8 ~
#> wx7 (b) 0.030 0.008 3.548 0.000
#> wy7 (a) 0.102 0.008 12.802 0.000
#> wy9 ~
#> wx8 (b) 0.030 0.008 3.548 0.000
#> wy8 (a) 0.102 0.008 12.802 0.000
#> wy10 ~
#> wx9 (b) 0.030 0.008 3.548 0.000
#> wy9 (a) 0.102 0.008 12.802 0.000
#> wy11 ~
#> wx10 (b) 0.030 0.008 3.548 0.000
#> wy10 (a) 0.102 0.008 12.802 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.052 0.013 4.087 0.000
#> .wx2 ~~
#> .wy2 0.047 0.013 3.720 0.000
#> .wx3 ~~
#> .wy3 0.030 0.011 2.687 0.007
#> .wx4 ~~
#> .wy4 0.045 0.011 4.062 0.000
#> .wx5 ~~
#> .wy5 0.044 0.011 4.057 0.000
#> .wx6 ~~
#> .wy6 0.026 0.011 2.404 0.016
#> .wx7 ~~
#> .wy7 0.034 0.011 2.992 0.003
#> .wx8 ~~
#> .wy8 0.032 0.011 2.834 0.005
#> .wx9 ~~
#> .wy9 0.012 0.013 0.959 0.337
#> .wx10 ~~
#> .wy10 0.048 0.013 3.688 0.000
#> .wx11 ~~
#> .wy11 0.062 0.013 4.865 0.000
#> .RIx ~~
#> .RIy 0.308 0.013 23.781 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.535 0.017 32.040 0.000
#> .RIy 0.500 0.016 31.781 0.000
#> wx1 0.449 0.019 23.866 0.000
#> wy1 0.374 0.016 23.272 0.000
#> .wx2 0.406 0.017 24.105 0.000
#> .wy2 0.428 0.017 24.616 0.000
#> .wx3 0.353 0.015 23.825 0.000
#> .wy3 0.319 0.014 23.389 0.000
#> .wx4 0.327 0.014 22.780 0.000
#> .wy4 0.328 0.014 22.674 0.000
#> .wx5 0.329 0.014 23.605 0.000
#> .wy5 0.337 0.014 23.534 0.000
#> .wx6 0.355 0.015 23.698 0.000
#> .wy6 0.308 0.013 23.315 0.000
#> .wx7 0.352 0.015 23.524 0.000
#> .wy7 0.332 0.014 23.601 0.000
#> .wx8 0.327 0.014 22.999 0.000
#> .wy8 0.331 0.014 23.197 0.000
#> .wx9 0.374 0.016 23.077 0.000
#> .wy9 0.376 0.016 22.787 0.000
#> .wx10 0.375 0.017 22.119 0.000
#> .wy10 0.343 0.016 21.618 0.000
#> .wx11 0.363 0.017 21.477 0.000
#> .wy11 0.329 0.016 20.681 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 57 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5881.742
#> Degrees of freedom 280
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.334 0.002 181.923 0.000
#> RIy ~
#> oply (e) 0.334 0.002 181.923 0.000
#> wx2 ~
#> wx1 (a) 0.116 0.008 14.473 0.000
#> wy1 (b) 0.042 0.008 4.918 0.000
#> wx3 ~
#> wx2 (a) 0.116 0.008 14.473 0.000
#> wy2 (b) 0.042 0.008 4.918 0.000
#> wx4 ~
#> wx3 (a) 0.116 0.008 14.473 0.000
#> wy3 (b) 0.042 0.008 4.918 0.000
#> wx5 ~
#> wx4 (a) 0.116 0.008 14.473 0.000
#> wy4 (b) 0.042 0.008 4.918 0.000
#> wx6 ~
#> wx5 (a) 0.116 0.008 14.473 0.000
#> wy5 (b) 0.042 0.008 4.918 0.000
#> wx7 ~
#> wx6 (a) 0.116 0.008 14.473 0.000
#> wy6 (b) 0.042 0.008 4.918 0.000
#> wx8 ~
#> wx7 (a) 0.116 0.008 14.473 0.000
#> wy7 (b) 0.042 0.008 4.918 0.000
#> wx9 ~
#> wx8 (a) 0.116 0.008 14.473 0.000
#> wy8 (b) 0.042 0.008 4.918 0.000
#> wx10 ~
#> wx9 (a) 0.116 0.008 14.473 0.000
#> wy9 (b) 0.042 0.008 4.918 0.000
#> wx11 ~
#> wx10 (a) 0.116 0.008 14.473 0.000
#> wy10 (b) 0.042 0.008 4.918 0.000
#> wy2 ~
#> wx1 (b) 0.042 0.008 4.918 0.000
#> wy1 (a) 0.116 0.008 14.473 0.000
#> wy3 ~
#> wx2 (b) 0.042 0.008 4.918 0.000
#> wy2 (a) 0.116 0.008 14.473 0.000
#> wy4 ~
#> wx3 (b) 0.042 0.008 4.918 0.000
#> wy3 (a) 0.116 0.008 14.473 0.000
#> wy5 ~
#> wx4 (b) 0.042 0.008 4.918 0.000
#> wy4 (a) 0.116 0.008 14.473 0.000
#> wy6 ~
#> wx5 (b) 0.042 0.008 4.918 0.000
#> wy5 (a) 0.116 0.008 14.473 0.000
#> wy7 ~
#> wx6 (b) 0.042 0.008 4.918 0.000
#> wy6 (a) 0.116 0.008 14.473 0.000
#> wy8 ~
#> wx7 (b) 0.042 0.008 4.918 0.000
#> wy7 (a) 0.116 0.008 14.473 0.000
#> wy9 ~
#> wx8 (b) 0.042 0.008 4.918 0.000
#> wy8 (a) 0.116 0.008 14.473 0.000
#> wy10 ~
#> wx9 (b) 0.042 0.008 4.918 0.000
#> wy9 (a) 0.116 0.008 14.473 0.000
#> wy11 ~
#> wx10 (b) 0.042 0.008 4.918 0.000
#> wy10 (a) 0.116 0.008 14.473 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.067 0.011 6.180 0.000
#> .wx2 ~~
#> .wy2 0.036 0.009 4.073 0.000
#> .wx3 ~~
#> .wy3 0.068 0.009 7.443 0.000
#> .wx4 ~~
#> .wy4 0.029 0.008 3.608 0.000
#> .wx5 ~~
#> .wy5 0.040 0.008 5.196 0.000
#> .wx6 ~~
#> .wy6 0.036 0.007 5.156 0.000
#> .wx7 ~~
#> .wy7 0.034 0.007 4.786 0.000
#> .wx8 ~~
#> .wy8 0.027 0.008 3.461 0.001
#> .wx9 ~~
#> .wy9 0.034 0.008 4.181 0.000
#> .wx10 ~~
#> .wy10 0.063 0.010 6.040 0.000
#> .wx11 ~~
#> .wy11 0.068 0.009 7.155 0.000
#> .RIx ~~
#> .RIy 1.081 0.039 27.517 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.608 0.043 37.197 0.000
#> .RIy 1.738 0.048 36.494 0.000
#> wx1 0.318 0.015 21.885 0.000
#> wy1 0.333 0.015 22.559 0.000
#> .wx2 0.295 0.013 22.916 0.000
#> .wy2 0.245 0.011 22.343 0.000
#> .wx3 0.264 0.011 23.389 0.000
#> .wy3 0.306 0.013 23.763 0.000
#> .wx4 0.219 0.010 22.181 0.000
#> .wy4 0.246 0.011 22.427 0.000
#> .wx5 0.249 0.011 22.940 0.000
#> .wy5 0.206 0.009 22.655 0.000
#> .wx6 0.219 0.010 22.441 0.000
#> .wy6 0.182 0.008 21.994 0.000
#> .wx7 0.210 0.009 22.603 0.000
#> .wy7 0.204 0.009 22.442 0.000
#> .wx8 0.218 0.010 22.064 0.000
#> .wy8 0.229 0.010 22.744 0.000
#> .wx9 0.248 0.011 22.330 0.000
#> .wy9 0.210 0.010 22.063 0.000
#> .wx10 0.280 0.013 21.647 0.000
#> .wy10 0.266 0.012 21.498 0.000
#> .wx11 0.257 0.012 20.889 0.000
#> .wy11 0.243 0.012 20.488 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 51 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 6298.286
#> Degrees of freedom 280
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.286 0.002 160.481 0.000
#> RIy ~
#> oply (e) 0.286 0.002 160.481 0.000
#> wx2 ~
#> wx1 (a) 0.121 0.008 14.959 0.000
#> wy1 (b) 0.007 0.009 0.845 0.398
#> wx3 ~
#> wx2 (a) 0.121 0.008 14.959 0.000
#> wy2 (b) 0.007 0.009 0.845 0.398
#> wx4 ~
#> wx3 (a) 0.121 0.008 14.959 0.000
#> wy3 (b) 0.007 0.009 0.845 0.398
#> wx5 ~
#> wx4 (a) 0.121 0.008 14.959 0.000
#> wy4 (b) 0.007 0.009 0.845 0.398
#> wx6 ~
#> wx5 (a) 0.121 0.008 14.959 0.000
#> wy5 (b) 0.007 0.009 0.845 0.398
#> wx7 ~
#> wx6 (a) 0.121 0.008 14.959 0.000
#> wy6 (b) 0.007 0.009 0.845 0.398
#> wx8 ~
#> wx7 (a) 0.121 0.008 14.959 0.000
#> wy7 (b) 0.007 0.009 0.845 0.398
#> wx9 ~
#> wx8 (a) 0.121 0.008 14.959 0.000
#> wy8 (b) 0.007 0.009 0.845 0.398
#> wx10 ~
#> wx9 (a) 0.121 0.008 14.959 0.000
#> wy9 (b) 0.007 0.009 0.845 0.398
#> wx11 ~
#> wx10 (a) 0.121 0.008 14.959 0.000
#> wy10 (b) 0.007 0.009 0.845 0.398
#> wy2 ~
#> wx1 (b) 0.007 0.009 0.845 0.398
#> wy1 (a) 0.121 0.008 14.959 0.000
#> wy3 ~
#> wx2 (b) 0.007 0.009 0.845 0.398
#> wy2 (a) 0.121 0.008 14.959 0.000
#> wy4 ~
#> wx3 (b) 0.007 0.009 0.845 0.398
#> wy3 (a) 0.121 0.008 14.959 0.000
#> wy5 ~
#> wx4 (b) 0.007 0.009 0.845 0.398
#> wy4 (a) 0.121 0.008 14.959 0.000
#> wy6 ~
#> wx5 (b) 0.007 0.009 0.845 0.398
#> wy5 (a) 0.121 0.008 14.959 0.000
#> wy7 ~
#> wx6 (b) 0.007 0.009 0.845 0.398
#> wy6 (a) 0.121 0.008 14.959 0.000
#> wy8 ~
#> wx7 (b) 0.007 0.009 0.845 0.398
#> wy7 (a) 0.121 0.008 14.959 0.000
#> wy9 ~
#> wx8 (b) 0.007 0.009 0.845 0.398
#> wy8 (a) 0.121 0.008 14.959 0.000
#> wy10 ~
#> wx9 (b) 0.007 0.009 0.845 0.398
#> wy9 (a) 0.121 0.008 14.959 0.000
#> wy11 ~
#> wx10 (b) 0.007 0.009 0.845 0.398
#> wy10 (a) 0.121 0.008 14.959 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.111 0.017 6.646 0.000
#> .wx2 ~~
#> .wy2 0.045 0.013 3.333 0.001
#> .wx3 ~~
#> .wy3 0.062 0.013 4.765 0.000
#> .wx4 ~~
#> .wy4 0.034 0.013 2.656 0.008
#> .wx5 ~~
#> .wy5 0.019 0.012 1.558 0.119
#> .wx6 ~~
#> .wy6 0.056 0.013 4.396 0.000
#> .wx7 ~~
#> .wy7 0.052 0.012 4.483 0.000
#> .wx8 ~~
#> .wy8 0.042 0.013 3.257 0.001
#> .wx9 ~~
#> .wy9 0.037 0.014 2.730 0.006
#> .wx10 ~~
#> .wy10 0.049 0.014 3.365 0.001
#> .wx11 ~~
#> .wy11 0.051 0.016 3.186 0.001
#> .RIx ~~
#> .RIy 0.999 0.036 27.380 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.570 0.043 36.219 0.000
#> .RIy 1.488 0.043 34.746 0.000
#> wx1 0.513 0.023 22.698 0.000
#> wy1 0.493 0.022 22.602 0.000
#> .wx2 0.409 0.018 22.994 0.000
#> .wy2 0.406 0.018 22.862 0.000
#> .wx3 0.398 0.017 23.436 0.000
#> .wy3 0.416 0.018 23.277 0.000
#> .wx4 0.379 0.017 22.322 0.000
#> .wy4 0.337 0.015 21.761 0.000
#> .wx5 0.348 0.015 22.775 0.000
#> .wy5 0.359 0.016 22.819 0.000
#> .wx6 0.383 0.017 23.183 0.000
#> .wy6 0.369 0.016 22.899 0.000
#> .wx7 0.365 0.016 22.978 0.000
#> .wy7 0.312 0.014 22.275 0.000
#> .wx8 0.362 0.016 22.679 0.000
#> .wy8 0.395 0.017 22.813 0.000
#> .wx9 0.390 0.017 22.479 0.000
#> .wy9 0.390 0.017 22.308 0.000
#> .wx10 0.377 0.018 21.329 0.000
#> .wy10 0.400 0.019 21.140 0.000
#> .wx11 0.454 0.021 21.540 0.000
#> .wy11 0.385 0.019 20.250 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.0003.6.4.3 SC-RI-CLPM
SCCLPM <- '
# Create between components
RIx =~ 1*x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11
RIy =~ 1*y1 + y2 + y3 + y4 + y5 + y6 + y7 + y8 + y9 + y10 + y11
RIx ~ e*oplx
RIy ~ e*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
wx2 ~ a*wx1 + b*wy1
wx3 ~ a*wx2 + b*wy2
wx4 ~ a*wx3 + b*wy3
wx5 ~ a*wx4 + b*wy4
wx6 ~ a*wx5 + b*wy5
wx7 ~ a*wx6 + b*wy6
wx8 ~ a*wx7 + b*wy7
wx9 ~ a*wx8 + b*wy8
wx10 ~ a*wx9 + b*wy9
wx11 ~ a*wx10 + b*wy10
wy2 ~ b*wx1 + a*wy1
wy3 ~ b*wx2 + a*wy2
wy4 ~ b*wx3 + a*wy3
wy5 ~ b*wx4 + a*wy4
wy6 ~ b*wx5 + a*wy5
wy7 ~ b*wx6 + a*wy6
wy8 ~ b*wx7 + a*wy7
wy9 ~ b*wx8 + a*wy8
wy10 ~ b*wx9 + a*wy9
wy11 ~ b*wx10 + a*wy10
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(SCCLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
results[[9]] <- results_temp[[1]]
results[[10]] <- results_temp[[2]]
results[[11]] <- results_temp[[3]]
results[[12]] <- results_temp[[4]]
names(results)[9:12] <- c("fitm3h1y1", "fitm3h1y2","fitm3h1y3","fitm3h1y4")load("addfiles/results.Rdata")
summary(results[[9]])
summary(results[[10]])
summary(results[[11]])
summary(results[[12]])#> lavaan 0.6-11 ended normally after 51 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1184.580
#> Degrees of freedom 260
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.032 0.015 70.760 0.000
#> x3 1.046 0.015 68.405 0.000
#> x4 0.917 0.015 59.630 0.000
#> x5 1.028 0.017 60.851 0.000
#> x6 0.936 0.015 61.616 0.000
#> x7 0.876 0.014 60.474 0.000
#> x8 0.919 0.015 60.197 0.000
#> x9 0.871 0.016 56.165 0.000
#> x10 0.944 0.016 58.963 0.000
#> x11 0.996 0.017 58.689 0.000
#> RIy =~
#> y1 1.000
#> y2 1.045 0.015 69.564 0.000
#> y3 1.059 0.016 66.061 0.000
#> y4 0.908 0.016 57.240 0.000
#> y5 0.919 0.016 56.258 0.000
#> y6 0.908 0.015 58.915 0.000
#> y7 0.863 0.015 57.729 0.000
#> y8 0.895 0.016 56.765 0.000
#> y9 0.899 0.016 55.775 0.000
#> y10 0.975 0.017 58.061 0.000
#> y11 1.022 0.018 57.752 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.127 0.002 79.687 0.000
#> RIy ~
#> oply (e) 0.127 0.002 79.687 0.000
#> wx2 ~
#> wx1 (a) 0.203 0.008 24.247 0.000
#> wy1 (b) 0.071 0.009 8.002 0.000
#> wx3 ~
#> wx2 (a) 0.203 0.008 24.247 0.000
#> wy2 (b) 0.071 0.009 8.002 0.000
#> wx4 ~
#> wx3 (a) 0.203 0.008 24.247 0.000
#> wy3 (b) 0.071 0.009 8.002 0.000
#> wx5 ~
#> wx4 (a) 0.203 0.008 24.247 0.000
#> wy4 (b) 0.071 0.009 8.002 0.000
#> wx6 ~
#> wx5 (a) 0.203 0.008 24.247 0.000
#> wy5 (b) 0.071 0.009 8.002 0.000
#> wx7 ~
#> wx6 (a) 0.203 0.008 24.247 0.000
#> wy6 (b) 0.071 0.009 8.002 0.000
#> wx8 ~
#> wx7 (a) 0.203 0.008 24.247 0.000
#> wy7 (b) 0.071 0.009 8.002 0.000
#> wx9 ~
#> wx8 (a) 0.203 0.008 24.247 0.000
#> wy8 (b) 0.071 0.009 8.002 0.000
#> wx10 ~
#> wx9 (a) 0.203 0.008 24.247 0.000
#> wy9 (b) 0.071 0.009 8.002 0.000
#> wx11 ~
#> wx10 (a) 0.203 0.008 24.247 0.000
#> wy10 (b) 0.071 0.009 8.002 0.000
#> wy2 ~
#> wx1 (b) 0.071 0.009 8.002 0.000
#> wy1 (a) 0.203 0.008 24.247 0.000
#> wy3 ~
#> wx2 (b) 0.071 0.009 8.002 0.000
#> wy2 (a) 0.203 0.008 24.247 0.000
#> wy4 ~
#> wx3 (b) 0.071 0.009 8.002 0.000
#> wy3 (a) 0.203 0.008 24.247 0.000
#> wy5 ~
#> wx4 (b) 0.071 0.009 8.002 0.000
#> wy4 (a) 0.203 0.008 24.247 0.000
#> wy6 ~
#> wx5 (b) 0.071 0.009 8.002 0.000
#> wy5 (a) 0.203 0.008 24.247 0.000
#> wy7 ~
#> wx6 (b) 0.071 0.009 8.002 0.000
#> wy6 (a) 0.203 0.008 24.247 0.000
#> wy8 ~
#> wx7 (b) 0.071 0.009 8.002 0.000
#> wy7 (a) 0.203 0.008 24.247 0.000
#> wy9 ~
#> wx8 (b) 0.071 0.009 8.002 0.000
#> wy8 (a) 0.203 0.008 24.247 0.000
#> wy10 ~
#> wx9 (b) 0.071 0.009 8.002 0.000
#> wy9 (a) 0.203 0.008 24.247 0.000
#> wy11 ~
#> wx10 (b) 0.071 0.009 8.002 0.000
#> wy10 (a) 0.203 0.008 24.247 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.105 0.022 4.761 0.000
#> .wx2 ~~
#> .wy2 0.090 0.020 4.528 0.000
#> .wx3 ~~
#> .wy3 0.088 0.018 4.821 0.000
#> .wx4 ~~
#> .wy4 0.103 0.018 5.617 0.000
#> .wx5 ~~
#> .wy5 0.103 0.021 4.820 0.000
#> .wx6 ~~
#> .wy6 0.072 0.017 4.327 0.000
#> .wx7 ~~
#> .wy7 0.087 0.015 5.705 0.000
#> .wx8 ~~
#> .wy8 0.082 0.018 4.524 0.000
#> .wx9 ~~
#> .wy9 0.098 0.019 5.111 0.000
#> .wx10 ~~
#> .wy10 0.038 0.020 1.893 0.058
#> .wx11 ~~
#> .wy11 0.088 0.020 4.313 0.000
#> .RIx ~~
#> .RIy 0.376 0.019 19.861 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.806 0.031 26.229 0.000
#> .RIy 0.520 0.021 24.305 0.000
#> wx1 0.696 0.031 22.335 0.000
#> wy1 0.601 0.027 21.922 0.000
#> .wx2 0.681 0.029 23.590 0.000
#> .wy2 0.555 0.024 22.682 0.000
#> .wx3 0.575 0.025 22.989 0.000
#> .wy3 0.491 0.022 22.059 0.000
#> .wx4 0.605 0.026 23.151 0.000
#> .wy4 0.488 0.022 22.431 0.000
#> .wx5 0.711 0.031 23.224 0.000
#> .wy5 0.573 0.024 23.432 0.000
#> .wx6 0.520 0.022 23.228 0.000
#> .wy6 0.438 0.019 22.472 0.000
#> .wx7 0.489 0.021 23.403 0.000
#> .wy7 0.441 0.019 23.043 0.000
#> .wx8 0.553 0.024 23.131 0.000
#> .wy8 0.508 0.022 23.022 0.000
#> .wx9 0.604 0.026 23.489 0.000
#> .wy9 0.516 0.023 22.406 0.000
#> .wx10 0.564 0.026 21.577 0.000
#> .wy10 0.502 0.024 20.981 0.000
#> .wx11 0.597 0.028 21.051 0.000
#> .wy11 0.495 0.025 20.035 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 44 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 745.392
#> Degrees of freedom 260
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000 0.014 70.278 0.000
#> x3 1.005 0.015 69.049 0.000
#> x4 1.008 0.015 67.174 0.000
#> x5 1.018 0.015 68.283 0.000
#> x6 1.003 0.015 65.205 0.000
#> x7 1.018 0.015 66.017 0.000
#> x8 0.977 0.015 65.373 0.000
#> x9 0.952 0.016 61.324 0.000
#> x10 1.015 0.016 62.772 0.000
#> x11 0.991 0.016 61.377 0.000
#> RIy =~
#> y1 1.000
#> y2 1.040 0.015 69.260 0.000
#> y3 1.072 0.015 71.615 0.000
#> y4 1.071 0.016 67.625 0.000
#> y5 1.077 0.016 68.626 0.000
#> y6 1.069 0.016 68.829 0.000
#> y7 1.069 0.016 67.652 0.000
#> y8 1.032 0.016 65.732 0.000
#> y9 1.020 0.016 61.914 0.000
#> y10 1.054 0.017 63.867 0.000
#> y11 1.062 0.017 63.216 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.102 0.001 80.150 0.000
#> RIy ~
#> oply (e) 0.102 0.001 80.150 0.000
#> wx2 ~
#> wx1 (a) 0.101 0.008 12.700 0.000
#> wy1 (b) 0.028 0.008 3.362 0.001
#> wx3 ~
#> wx2 (a) 0.101 0.008 12.700 0.000
#> wy2 (b) 0.028 0.008 3.362 0.001
#> wx4 ~
#> wx3 (a) 0.101 0.008 12.700 0.000
#> wy3 (b) 0.028 0.008 3.362 0.001
#> wx5 ~
#> wx4 (a) 0.101 0.008 12.700 0.000
#> wy4 (b) 0.028 0.008 3.362 0.001
#> wx6 ~
#> wx5 (a) 0.101 0.008 12.700 0.000
#> wy5 (b) 0.028 0.008 3.362 0.001
#> wx7 ~
#> wx6 (a) 0.101 0.008 12.700 0.000
#> wy6 (b) 0.028 0.008 3.362 0.001
#> wx8 ~
#> wx7 (a) 0.101 0.008 12.700 0.000
#> wy7 (b) 0.028 0.008 3.362 0.001
#> wx9 ~
#> wx8 (a) 0.101 0.008 12.700 0.000
#> wy8 (b) 0.028 0.008 3.362 0.001
#> wx10 ~
#> wx9 (a) 0.101 0.008 12.700 0.000
#> wy9 (b) 0.028 0.008 3.362 0.001
#> wx11 ~
#> wx10 (a) 0.101 0.008 12.700 0.000
#> wy10 (b) 0.028 0.008 3.362 0.001
#> wy2 ~
#> wx1 (b) 0.028 0.008 3.362 0.001
#> wy1 (a) 0.101 0.008 12.700 0.000
#> wy3 ~
#> wx2 (b) 0.028 0.008 3.362 0.001
#> wy2 (a) 0.101 0.008 12.700 0.000
#> wy4 ~
#> wx3 (b) 0.028 0.008 3.362 0.001
#> wy3 (a) 0.101 0.008 12.700 0.000
#> wy5 ~
#> wx4 (b) 0.028 0.008 3.362 0.001
#> wy4 (a) 0.101 0.008 12.700 0.000
#> wy6 ~
#> wx5 (b) 0.028 0.008 3.362 0.001
#> wy5 (a) 0.101 0.008 12.700 0.000
#> wy7 ~
#> wx6 (b) 0.028 0.008 3.362 0.001
#> wy6 (a) 0.101 0.008 12.700 0.000
#> wy8 ~
#> wx7 (b) 0.028 0.008 3.362 0.001
#> wy7 (a) 0.101 0.008 12.700 0.000
#> wy9 ~
#> wx8 (b) 0.028 0.008 3.362 0.001
#> wy8 (a) 0.101 0.008 12.700 0.000
#> wy10 ~
#> wx9 (b) 0.028 0.008 3.362 0.001
#> wy9 (a) 0.101 0.008 12.700 0.000
#> wy11 ~
#> wx10 (b) 0.028 0.008 3.362 0.001
#> wy10 (a) 0.101 0.008 12.700 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.050 0.013 3.930 0.000
#> .wx2 ~~
#> .wy2 0.047 0.013 3.703 0.000
#> .wx3 ~~
#> .wy3 0.030 0.011 2.673 0.008
#> .wx4 ~~
#> .wy4 0.043 0.011 3.898 0.000
#> .wx5 ~~
#> .wy5 0.043 0.011 3.948 0.000
#> .wx6 ~~
#> .wy6 0.026 0.011 2.376 0.017
#> .wx7 ~~
#> .wy7 0.032 0.011 2.881 0.004
#> .wx8 ~~
#> .wy8 0.030 0.011 2.717 0.007
#> .wx9 ~~
#> .wy9 0.010 0.013 0.761 0.447
#> .wx10 ~~
#> .wy10 0.045 0.013 3.478 0.001
#> .wx11 ~~
#> .wy11 0.062 0.013 4.871 0.000
#> .RIx ~~
#> .RIy 0.297 0.013 22.520 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.535 0.019 27.861 0.000
#> .RIy 0.451 0.017 27.154 0.000
#> wx1 0.448 0.019 23.890 0.000
#> wy1 0.387 0.017 23.322 0.000
#> .wx2 0.407 0.017 23.992 0.000
#> .wy2 0.428 0.017 24.549 0.000
#> .wx3 0.352 0.015 23.687 0.000
#> .wy3 0.315 0.014 23.088 0.000
#> .wx4 0.326 0.014 22.627 0.000
#> .wy4 0.325 0.014 22.443 0.000
#> .wx5 0.327 0.014 23.360 0.000
#> .wy5 0.333 0.014 23.306 0.000
#> .wx6 0.355 0.015 23.631 0.000
#> .wy6 0.306 0.013 23.113 0.000
#> .wx7 0.349 0.015 23.310 0.000
#> .wy7 0.330 0.014 23.423 0.000
#> .wx8 0.328 0.014 23.096 0.000
#> .wy8 0.333 0.014 23.284 0.000
#> .wx9 0.374 0.016 23.256 0.000
#> .wy9 0.377 0.016 22.894 0.000
#> .wx10 0.370 0.017 21.778 0.000
#> .wy10 0.343 0.016 21.456 0.000
#> .wx11 0.365 0.017 21.452 0.000
#> .wy11 0.326 0.016 20.501 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 94 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5754.776
#> Degrees of freedom 260
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.995 0.004 241.929 0.000
#> x3 0.993 0.004 232.141 0.000
#> x4 1.001 0.004 231.154 0.000
#> x5 1.003 0.004 227.019 0.000
#> x6 1.008 0.004 231.190 0.000
#> x7 1.013 0.004 233.021 0.000
#> x8 1.016 0.004 228.624 0.000
#> x9 1.008 0.005 218.153 0.000
#> x10 1.004 0.005 208.323 0.000
#> x11 1.014 0.005 208.580 0.000
#> RIy =~
#> y1 1.000
#> y2 1.015 0.004 251.843 0.000
#> y3 1.011 0.005 221.550 0.000
#> y4 1.023 0.005 224.154 0.000
#> y5 1.028 0.004 234.838 0.000
#> y6 1.030 0.004 237.318 0.000
#> y7 1.033 0.004 232.516 0.000
#> y8 1.035 0.005 224.870 0.000
#> y9 1.028 0.005 224.226 0.000
#> y10 1.024 0.005 208.550 0.000
#> y11 1.034 0.005 208.052 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.330 0.002 168.741 0.000
#> RIy ~
#> oply (e) 0.330 0.002 168.741 0.000
#> wx2 ~
#> wx1 (a) 0.112 0.008 14.014 0.000
#> wy1 (b) 0.037 0.008 4.430 0.000
#> wx3 ~
#> wx2 (a) 0.112 0.008 14.014 0.000
#> wy2 (b) 0.037 0.008 4.430 0.000
#> wx4 ~
#> wx3 (a) 0.112 0.008 14.014 0.000
#> wy3 (b) 0.037 0.008 4.430 0.000
#> wx5 ~
#> wx4 (a) 0.112 0.008 14.014 0.000
#> wy4 (b) 0.037 0.008 4.430 0.000
#> wx6 ~
#> wx5 (a) 0.112 0.008 14.014 0.000
#> wy5 (b) 0.037 0.008 4.430 0.000
#> wx7 ~
#> wx6 (a) 0.112 0.008 14.014 0.000
#> wy6 (b) 0.037 0.008 4.430 0.000
#> wx8 ~
#> wx7 (a) 0.112 0.008 14.014 0.000
#> wy7 (b) 0.037 0.008 4.430 0.000
#> wx9 ~
#> wx8 (a) 0.112 0.008 14.014 0.000
#> wy8 (b) 0.037 0.008 4.430 0.000
#> wx10 ~
#> wx9 (a) 0.112 0.008 14.014 0.000
#> wy9 (b) 0.037 0.008 4.430 0.000
#> wx11 ~
#> wx10 (a) 0.112 0.008 14.014 0.000
#> wy10 (b) 0.037 0.008 4.430 0.000
#> wy2 ~
#> wx1 (b) 0.037 0.008 4.430 0.000
#> wy1 (a) 0.112 0.008 14.014 0.000
#> wy3 ~
#> wx2 (b) 0.037 0.008 4.430 0.000
#> wy2 (a) 0.112 0.008 14.014 0.000
#> wy4 ~
#> wx3 (b) 0.037 0.008 4.430 0.000
#> wy3 (a) 0.112 0.008 14.014 0.000
#> wy5 ~
#> wx4 (b) 0.037 0.008 4.430 0.000
#> wy4 (a) 0.112 0.008 14.014 0.000
#> wy6 ~
#> wx5 (b) 0.037 0.008 4.430 0.000
#> wy5 (a) 0.112 0.008 14.014 0.000
#> wy7 ~
#> wx6 (b) 0.037 0.008 4.430 0.000
#> wy6 (a) 0.112 0.008 14.014 0.000
#> wy8 ~
#> wx7 (b) 0.037 0.008 4.430 0.000
#> wy7 (a) 0.112 0.008 14.014 0.000
#> wy9 ~
#> wx8 (b) 0.037 0.008 4.430 0.000
#> wy8 (a) 0.112 0.008 14.014 0.000
#> wy10 ~
#> wx9 (b) 0.037 0.008 4.430 0.000
#> wy9 (a) 0.112 0.008 14.014 0.000
#> wy11 ~
#> wx10 (b) 0.037 0.008 4.430 0.000
#> wy10 (a) 0.112 0.008 14.014 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.063 0.011 5.802 0.000
#> .wx2 ~~
#> .wy2 0.035 0.009 3.985 0.000
#> .wx3 ~~
#> .wy3 0.066 0.009 7.321 0.000
#> .wx4 ~~
#> .wy4 0.029 0.008 3.610 0.000
#> .wx5 ~~
#> .wy5 0.040 0.008 5.149 0.000
#> .wx6 ~~
#> .wy6 0.035 0.007 5.062 0.000
#> .wx7 ~~
#> .wy7 0.032 0.007 4.544 0.000
#> .wx8 ~~
#> .wy8 0.024 0.008 3.085 0.002
#> .wx9 ~~
#> .wy9 0.034 0.008 4.193 0.000
#> .wx10 ~~
#> .wy10 0.062 0.010 6.033 0.000
#> .wx11 ~~
#> .wy11 0.066 0.009 6.958 0.000
#> .RIx ~~
#> .RIy 1.057 0.038 27.498 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.603 0.044 36.255 0.000
#> .RIy 1.651 0.046 35.668 0.000
#> wx1 0.316 0.014 21.886 0.000
#> wy1 0.332 0.015 22.517 0.000
#> .wx2 0.294 0.013 22.946 0.000
#> .wy2 0.244 0.011 22.349 0.000
#> .wx3 0.262 0.011 23.429 0.000
#> .wy3 0.304 0.013 23.807 0.000
#> .wx4 0.219 0.010 22.197 0.000
#> .wy4 0.245 0.011 22.431 0.000
#> .wx5 0.249 0.011 22.961 0.000
#> .wy5 0.204 0.009 22.632 0.000
#> .wx6 0.219 0.010 22.422 0.000
#> .wy6 0.180 0.008 21.944 0.000
#> .wx7 0.209 0.009 22.518 0.000
#> .wy7 0.202 0.009 22.378 0.000
#> .wx8 0.215 0.010 21.933 0.000
#> .wy8 0.226 0.010 22.647 0.000
#> .wx9 0.248 0.011 22.337 0.000
#> .wy9 0.210 0.010 22.065 0.000
#> .wx10 0.279 0.013 21.674 0.000
#> .wy10 0.266 0.012 21.520 0.000
#> .wx11 0.255 0.012 20.788 0.000
#> .wy11 0.240 0.012 20.376 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 67 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 39
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 6116.744
#> Degrees of freedom 260
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.991 0.006 172.616 0.000
#> x3 0.989 0.006 162.821 0.000
#> x4 0.989 0.006 157.453 0.000
#> x5 1.016 0.006 164.159 0.000
#> x6 0.988 0.006 157.004 0.000
#> x7 0.992 0.006 158.043 0.000
#> x8 1.003 0.006 157.073 0.000
#> x9 1.012 0.007 152.846 0.000
#> x10 1.013 0.007 151.056 0.000
#> x11 1.024 0.007 142.513 0.000
#> RIy =~
#> y1 1.000
#> y2 1.041 0.006 175.131 0.000
#> y3 1.031 0.006 160.421 0.000
#> y4 1.041 0.006 162.313 0.000
#> y5 1.056 0.006 163.112 0.000
#> y6 1.035 0.007 158.293 0.000
#> y7 1.030 0.006 162.578 0.000
#> y8 1.040 0.007 154.358 0.000
#> y9 1.039 0.007 151.676 0.000
#> y10 1.033 0.007 147.337 0.000
#> y11 1.036 0.007 144.519 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.281 0.002 142.213 0.000
#> RIy ~
#> oply (e) 0.281 0.002 142.213 0.000
#> wx2 ~
#> wx1 (a) 0.119 0.008 14.812 0.000
#> wy1 (b) 0.009 0.009 1.067 0.286
#> wx3 ~
#> wx2 (a) 0.119 0.008 14.812 0.000
#> wy2 (b) 0.009 0.009 1.067 0.286
#> wx4 ~
#> wx3 (a) 0.119 0.008 14.812 0.000
#> wy3 (b) 0.009 0.009 1.067 0.286
#> wx5 ~
#> wx4 (a) 0.119 0.008 14.812 0.000
#> wy4 (b) 0.009 0.009 1.067 0.286
#> wx6 ~
#> wx5 (a) 0.119 0.008 14.812 0.000
#> wy5 (b) 0.009 0.009 1.067 0.286
#> wx7 ~
#> wx6 (a) 0.119 0.008 14.812 0.000
#> wy6 (b) 0.009 0.009 1.067 0.286
#> wx8 ~
#> wx7 (a) 0.119 0.008 14.812 0.000
#> wy7 (b) 0.009 0.009 1.067 0.286
#> wx9 ~
#> wx8 (a) 0.119 0.008 14.812 0.000
#> wy8 (b) 0.009 0.009 1.067 0.286
#> wx10 ~
#> wx9 (a) 0.119 0.008 14.812 0.000
#> wy9 (b) 0.009 0.009 1.067 0.286
#> wx11 ~
#> wx10 (a) 0.119 0.008 14.812 0.000
#> wy10 (b) 0.009 0.009 1.067 0.286
#> wy2 ~
#> wx1 (b) 0.009 0.009 1.067 0.286
#> wy1 (a) 0.119 0.008 14.812 0.000
#> wy3 ~
#> wx2 (b) 0.009 0.009 1.067 0.286
#> wy2 (a) 0.119 0.008 14.812 0.000
#> wy4 ~
#> wx3 (b) 0.009 0.009 1.067 0.286
#> wy3 (a) 0.119 0.008 14.812 0.000
#> wy5 ~
#> wx4 (b) 0.009 0.009 1.067 0.286
#> wy4 (a) 0.119 0.008 14.812 0.000
#> wy6 ~
#> wx5 (b) 0.009 0.009 1.067 0.286
#> wy5 (a) 0.119 0.008 14.812 0.000
#> wy7 ~
#> wx6 (b) 0.009 0.009 1.067 0.286
#> wy6 (a) 0.119 0.008 14.812 0.000
#> wy8 ~
#> wx7 (b) 0.009 0.009 1.067 0.286
#> wy7 (a) 0.119 0.008 14.812 0.000
#> wy9 ~
#> wx8 (b) 0.009 0.009 1.067 0.286
#> wy8 (a) 0.119 0.008 14.812 0.000
#> wy10 ~
#> wx9 (b) 0.009 0.009 1.067 0.286
#> wy9 (a) 0.119 0.008 14.812 0.000
#> wy11 ~
#> wx10 (b) 0.009 0.009 1.067 0.286
#> wy10 (a) 0.119 0.008 14.812 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.099 0.017 5.902 0.000
#> .wx2 ~~
#> .wy2 0.047 0.013 3.526 0.000
#> .wx3 ~~
#> .wy3 0.063 0.013 4.792 0.000
#> .wx4 ~~
#> .wy4 0.037 0.013 2.841 0.005
#> .wx5 ~~
#> .wy5 0.009 0.012 0.756 0.450
#> .wx6 ~~
#> .wy6 0.057 0.013 4.538 0.000
#> .wx7 ~~
#> .wy7 0.053 0.012 4.517 0.000
#> .wx8 ~~
#> .wy8 0.042 0.013 3.259 0.001
#> .wx9 ~~
#> .wy9 0.037 0.014 2.714 0.007
#> .wx10 ~~
#> .wy10 0.050 0.014 3.474 0.001
#> .wx11 ~~
#> .wy11 0.048 0.016 3.034 0.002
#> .RIx ~~
#> .RIy 0.979 0.036 27.320 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.575 0.045 34.743 0.000
#> .RIy 1.372 0.041 33.292 0.000
#> wx1 0.511 0.023 22.541 0.000
#> wy1 0.511 0.023 22.456 0.000
#> .wx2 0.410 0.018 23.033 0.000
#> .wy2 0.398 0.017 22.725 0.000
#> .wx3 0.398 0.017 23.489 0.000
#> .wy3 0.417 0.018 23.305 0.000
#> .wx4 0.379 0.017 22.390 0.000
#> .wy4 0.335 0.015 21.696 0.000
#> .wx5 0.341 0.015 22.554 0.000
#> .wy5 0.348 0.015 22.574 0.000
#> .wx6 0.381 0.016 23.268 0.000
#> .wy6 0.371 0.016 22.940 0.000
#> .wx7 0.364 0.016 23.035 0.000
#> .wy7 0.313 0.014 22.330 0.000
#> .wx8 0.361 0.016 22.670 0.000
#> .wy8 0.394 0.017 22.772 0.000
#> .wx9 0.387 0.017 22.395 0.000
#> .wy9 0.389 0.017 22.283 0.000
#> .wx10 0.375 0.018 21.249 0.000
#> .wy10 0.400 0.019 21.157 0.000
#> .wx11 0.443 0.021 21.352 0.000
#> .wy11 0.384 0.019 20.226 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.0003.6.4.4 LT-RI-CLPM
LTRICLPM <- '
# Create between components (random intercepts)
RIx =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11
RIy =~ 1*y1 + 1*y2 + 1*y3 + 1*y4 + 1*y5 + 1*y6 + 1*y7 + 1*y8 + 1*y9 + 1*y10 + 1*y11
RIx ~ e*oplx
RIy ~ e*oply
#Random slopes
RIsx =~ 1*x1 + 2*x2 + 3*x3 + 4*x4 + 5*x5 + 6*x6 + 7*x7 + 8*x8 + 9*x9 + 10*x10 + 11*x11
RIsy =~ 1*y1 + 2*y2 + 3*y3 + 4*y4 + 5*y5 + 6*y6 + 7*y7 + 8*y8 + 9*y9 + 10*y10 + 11*y11
RIsx ~ f*oplx
RIsy ~ f*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
wx2 ~ a*wx1 + b*wy1
wx3 ~ a*wx2 + b*wy2
wx4 ~ a*wx3 + b*wy3
wx5 ~ a*wx4 + b*wy4
wx6 ~ a*wx5 + b*wy5
wx7 ~ a*wx6 + b*wy6
wx8 ~ a*wx7 + b*wy7
wx9 ~ a*wx8 + b*wy8
wx10 ~ a*wx9 + b*wy9
wx11 ~ a*wx10 + b*wy10
wy2 ~ b*wx1 + a*wy1
wy3 ~ b*wx2 + a*wy2
wy4 ~ b*wx3 + a*wy3
wy5 ~ b*wx4 + a*wy4
wy6 ~ b*wx5 + a*wy5
wy7 ~ b*wx6 + a*wy6
wy8 ~ b*wx7 + a*wy7
wy9 ~ b*wx8 + a*wy8
wy10 ~ b*wx9 + a*wy9
wy11 ~ b*wx10 + a*wy10
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts and random slopes.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy #covariance intercepts: interpretation SELECTION
RIsx ~~ RIsx
RIsy ~~ RIsy
RIsx ~~ RIsy #covariance slopes: interpretation COMMON CONTEXT
RIx ~~ RIsx #covariance intercept/slope: interpretation regression to the mean
RIy ~~ RIsy
RIx ~~ RIsy #cross-covariance: interpretation INFLUENCE?
RIy ~~ RIsx
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(LTRICLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
results[[13]] <- results_temp[[1]]
results[[14]] <- results_temp[[2]]
results[[15]] <- results_temp[[3]]
results[[16]] <- results_temp[[4]]
names(results)[9:12] <- c("fitm4h1y1", "fitm4h1y2","fitm4h1y3","fitm4h1y4")
save(results, file="results.RData")load("addfiles/results.Rdata")
summary(results[[13]])
summary(results[[14]])
summary(results[[15]])
summary(results[[16]])#> lavaan 0.6-11 ended normally after 86 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 40
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1387.507
#> Degrees of freedom 272
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.132 0.001 91.424 0.000
#> RIy ~
#> oply (e) 0.132 0.001 91.424 0.000
#> RIsx ~
#> oplx (f) -0.002 0.000 -9.935 0.000
#> RIsy ~
#> oply (f) -0.002 0.000 -9.935 0.000
#> wx2 ~
#> wx1 (a) 0.145 0.010 14.885 0.000
#> wy1 (b) 0.058 0.010 5.674 0.000
#> wx3 ~
#> wx2 (a) 0.145 0.010 14.885 0.000
#> wy2 (b) 0.058 0.010 5.674 0.000
#> wx4 ~
#> wx3 (a) 0.145 0.010 14.885 0.000
#> wy3 (b) 0.058 0.010 5.674 0.000
#> wx5 ~
#> wx4 (a) 0.145 0.010 14.885 0.000
#> wy4 (b) 0.058 0.010 5.674 0.000
#> wx6 ~
#> wx5 (a) 0.145 0.010 14.885 0.000
#> wy5 (b) 0.058 0.010 5.674 0.000
#> wx7 ~
#> wx6 (a) 0.145 0.010 14.885 0.000
#> wy6 (b) 0.058 0.010 5.674 0.000
#> wx8 ~
#> wx7 (a) 0.145 0.010 14.885 0.000
#> wy7 (b) 0.058 0.010 5.674 0.000
#> wx9 ~
#> wx8 (a) 0.145 0.010 14.885 0.000
#> wy8 (b) 0.058 0.010 5.674 0.000
#> wx10 ~
#> wx9 (a) 0.145 0.010 14.885 0.000
#> wy9 (b) 0.058 0.010 5.674 0.000
#> wx11 ~
#> wx10 (a) 0.145 0.010 14.885 0.000
#> wy10 (b) 0.058 0.010 5.674 0.000
#> wy2 ~
#> wx1 (b) 0.058 0.010 5.674 0.000
#> wy1 (a) 0.145 0.010 14.885 0.000
#> wy3 ~
#> wx2 (b) 0.058 0.010 5.674 0.000
#> wy2 (a) 0.145 0.010 14.885 0.000
#> wy4 ~
#> wx3 (b) 0.058 0.010 5.674 0.000
#> wy3 (a) 0.145 0.010 14.885 0.000
#> wy5 ~
#> wx4 (b) 0.058 0.010 5.674 0.000
#> wy4 (a) 0.145 0.010 14.885 0.000
#> wy6 ~
#> wx5 (b) 0.058 0.010 5.674 0.000
#> wy5 (a) 0.145 0.010 14.885 0.000
#> wy7 ~
#> wx6 (b) 0.058 0.010 5.674 0.000
#> wy6 (a) 0.145 0.010 14.885 0.000
#> wy8 ~
#> wx7 (b) 0.058 0.010 5.674 0.000
#> wy7 (a) 0.145 0.010 14.885 0.000
#> wy9 ~
#> wx8 (b) 0.058 0.010 5.674 0.000
#> wy8 (a) 0.145 0.010 14.885 0.000
#> wy10 ~
#> wx9 (b) 0.058 0.010 5.674 0.000
#> wy9 (a) 0.145 0.010 14.885 0.000
#> wy11 ~
#> wx10 (b) 0.058 0.010 5.674 0.000
#> wy10 (a) 0.145 0.010 14.885 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.093 0.023 4.098 0.000
#> .wx2 ~~
#> .wy2 0.090 0.020 4.521 0.000
#> .wx3 ~~
#> .wy3 0.110 0.019 5.912 0.000
#> .wx4 ~~
#> .wy4 0.111 0.019 5.894 0.000
#> .wx5 ~~
#> .wy5 0.095 0.021 4.460 0.000
#> .wx6 ~~
#> .wy6 0.065 0.016 4.046 0.000
#> .wx7 ~~
#> .wy7 0.083 0.015 5.458 0.000
#> .wx8 ~~
#> .wy8 0.072 0.018 4.054 0.000
#> .wx9 ~~
#> .wy9 0.080 0.019 4.260 0.000
#> .wx10 ~~
#> .wy10 0.047 0.021 2.275 0.023
#> .wx11 ~~
#> .wy11 0.110 0.022 4.958 0.000
#> .RIx ~~
#> .RIy 0.294 0.027 10.860 0.000
#> .RIsx ~~
#> .RIsy 0.001 0.000 2.509 0.012
#> .RIx ~~
#> .RIsx -0.014 0.004 -3.372 0.001
#> .RIy ~~
#> .RIsy -0.005 0.003 -1.453 0.146
#> .RIx ~~
#> .RIsy 0.003 0.003 0.762 0.446
#> .RIy ~~
#> .RIsx 0.003 0.003 0.931 0.352
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.775 0.040 19.367 0.000
#> .RIy 0.483 0.031 15.779 0.000
#> .RIsx 0.005 0.001 7.510 0.000
#> .RIsy 0.002 0.000 4.589 0.000
#> wx1 0.613 0.031 19.513 0.000
#> wy1 0.566 0.028 20.232 0.000
#> .wx2 0.648 0.028 22.850 0.000
#> .wy2 0.545 0.024 22.400 0.000
#> .wx3 0.577 0.025 23.074 0.000
#> .wy3 0.509 0.023 22.501 0.000
#> .wx4 0.588 0.026 22.408 0.000
#> .wy4 0.481 0.022 21.760 0.000
#> .wx5 0.730 0.031 23.908 0.000
#> .wy5 0.557 0.024 23.263 0.000
#> .wx6 0.498 0.022 22.911 0.000
#> .wy6 0.417 0.019 22.078 0.000
#> .wx7 0.460 0.021 22.404 0.000
#> .wy7 0.427 0.019 22.272 0.000
#> .wx8 0.516 0.023 22.410 0.000
#> .wy8 0.485 0.022 22.333 0.000
#> .wx9 0.551 0.025 21.848 0.000
#> .wy9 0.474 0.022 21.162 0.000
#> .wx10 0.516 0.026 19.884 0.000
#> .wy10 0.491 0.025 19.977 0.000
#> .wx11 0.563 0.029 19.152 0.000
#> .wy11 0.504 0.027 18.572 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 122 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 40
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 753.109
#> Degrees of freedom 272
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.103 0.001 80.062 0.000
#> RIy ~
#> oply (e) 0.103 0.001 80.062 0.000
#> RIsx ~
#> oplx (f) 0.000 0.000 1.452 0.146
#> RIsy ~
#> oply (f) 0.000 0.000 1.452 0.146
#> wx2 ~
#> wx1 (a) 0.066 0.009 7.261 0.000
#> wy1 (b) 0.015 0.009 1.542 0.123
#> wx3 ~
#> wx2 (a) 0.066 0.009 7.261 0.000
#> wy2 (b) 0.015 0.009 1.542 0.123
#> wx4 ~
#> wx3 (a) 0.066 0.009 7.261 0.000
#> wy3 (b) 0.015 0.009 1.542 0.123
#> wx5 ~
#> wx4 (a) 0.066 0.009 7.261 0.000
#> wy4 (b) 0.015 0.009 1.542 0.123
#> wx6 ~
#> wx5 (a) 0.066 0.009 7.261 0.000
#> wy5 (b) 0.015 0.009 1.542 0.123
#> wx7 ~
#> wx6 (a) 0.066 0.009 7.261 0.000
#> wy6 (b) 0.015 0.009 1.542 0.123
#> wx8 ~
#> wx7 (a) 0.066 0.009 7.261 0.000
#> wy7 (b) 0.015 0.009 1.542 0.123
#> wx9 ~
#> wx8 (a) 0.066 0.009 7.261 0.000
#> wy8 (b) 0.015 0.009 1.542 0.123
#> wx10 ~
#> wx9 (a) 0.066 0.009 7.261 0.000
#> wy9 (b) 0.015 0.009 1.542 0.123
#> wx11 ~
#> wx10 (a) 0.066 0.009 7.261 0.000
#> wy10 (b) 0.015 0.009 1.542 0.123
#> wy2 ~
#> wx1 (b) 0.015 0.009 1.542 0.123
#> wy1 (a) 0.066 0.009 7.261 0.000
#> wy3 ~
#> wx2 (b) 0.015 0.009 1.542 0.123
#> wy2 (a) 0.066 0.009 7.261 0.000
#> wy4 ~
#> wx3 (b) 0.015 0.009 1.542 0.123
#> wy3 (a) 0.066 0.009 7.261 0.000
#> wy5 ~
#> wx4 (b) 0.015 0.009 1.542 0.123
#> wy4 (a) 0.066 0.009 7.261 0.000
#> wy6 ~
#> wx5 (b) 0.015 0.009 1.542 0.123
#> wy5 (a) 0.066 0.009 7.261 0.000
#> wy7 ~
#> wx6 (b) 0.015 0.009 1.542 0.123
#> wy6 (a) 0.066 0.009 7.261 0.000
#> wy8 ~
#> wx7 (b) 0.015 0.009 1.542 0.123
#> wy7 (a) 0.066 0.009 7.261 0.000
#> wy9 ~
#> wx8 (b) 0.015 0.009 1.542 0.123
#> wy8 (a) 0.066 0.009 7.261 0.000
#> wy10 ~
#> wx9 (b) 0.015 0.009 1.542 0.123
#> wy9 (a) 0.066 0.009 7.261 0.000
#> wy11 ~
#> wx10 (b) 0.015 0.009 1.542 0.123
#> wy10 (a) 0.066 0.009 7.261 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.030 0.013 2.313 0.021
#> .wx2 ~~
#> .wy2 0.041 0.013 3.195 0.001
#> .wx3 ~~
#> .wy3 0.020 0.011 1.832 0.067
#> .wx4 ~~
#> .wy4 0.039 0.011 3.589 0.000
#> .wx5 ~~
#> .wy5 0.041 0.011 3.808 0.000
#> .wx6 ~~
#> .wy6 0.024 0.011 2.233 0.026
#> .wx7 ~~
#> .wy7 0.032 0.011 2.814 0.005
#> .wx8 ~~
#> .wy8 0.027 0.011 2.402 0.016
#> .wx9 ~~
#> .wy9 0.009 0.013 0.744 0.457
#> .wx10 ~~
#> .wy10 0.038 0.013 2.986 0.003
#> .wx11 ~~
#> .wy11 0.052 0.013 3.997 0.000
#> .RIx ~~
#> .RIy 0.379 0.021 18.233 0.000
#> .RIsx ~~
#> .RIsy 0.001 0.000 3.498 0.000
#> .RIx ~~
#> .RIsx -0.011 0.002 -4.796 0.000
#> .RIy ~~
#> .RIsy -0.014 0.002 -6.106 0.000
#> .RIx ~~
#> .RIsy -0.010 0.002 -4.812 0.000
#> .RIy ~~
#> .RIsx -0.006 0.002 -3.087 0.002
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.619 0.027 23.131 0.000
#> .RIy 0.613 0.026 23.241 0.000
#> .RIsx 0.001 0.000 5.094 0.000
#> .RIsy 0.002 0.000 5.690 0.000
#> wx1 0.410 0.019 21.642 0.000
#> wy1 0.332 0.016 20.354 0.000
#> .wx2 0.389 0.017 22.962 0.000
#> .wy2 0.410 0.017 23.591 0.000
#> .wx3 0.338 0.015 23.049 0.000
#> .wy3 0.304 0.013 22.542 0.000
#> .wx4 0.317 0.014 22.420 0.000
#> .wy4 0.318 0.014 22.330 0.000
#> .wx5 0.325 0.014 23.514 0.000
#> .wy5 0.332 0.014 23.431 0.000
#> .wx6 0.350 0.015 23.649 0.000
#> .wy6 0.304 0.013 23.244 0.000
#> .wx7 0.348 0.015 23.436 0.000
#> .wy7 0.327 0.014 23.469 0.000
#> .wx8 0.318 0.014 22.681 0.000
#> .wy8 0.322 0.014 22.854 0.000
#> .wx9 0.365 0.016 22.530 0.000
#> .wy9 0.364 0.016 22.194 0.000
#> .wx10 0.352 0.017 20.833 0.000
#> .wy10 0.322 0.016 20.438 0.000
#> .wx11 0.342 0.017 19.837 0.000
#> .wy11 0.304 0.016 18.850 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 107 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 40
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5704.541
#> Degrees of freedom 272
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.330 0.002 166.688 0.000
#> RIy ~
#> oply (e) 0.330 0.002 166.688 0.000
#> RIsx ~
#> oplx (f) 0.001 0.000 6.280 0.000
#> RIsy ~
#> oply (f) 0.001 0.000 6.280 0.000
#> wx2 ~
#> wx1 (a) 0.060 0.009 6.641 0.000
#> wy1 (b) 0.033 0.009 3.485 0.000
#> wx3 ~
#> wx2 (a) 0.060 0.009 6.641 0.000
#> wy2 (b) 0.033 0.009 3.485 0.000
#> wx4 ~
#> wx3 (a) 0.060 0.009 6.641 0.000
#> wy3 (b) 0.033 0.009 3.485 0.000
#> wx5 ~
#> wx4 (a) 0.060 0.009 6.641 0.000
#> wy4 (b) 0.033 0.009 3.485 0.000
#> wx6 ~
#> wx5 (a) 0.060 0.009 6.641 0.000
#> wy5 (b) 0.033 0.009 3.485 0.000
#> wx7 ~
#> wx6 (a) 0.060 0.009 6.641 0.000
#> wy6 (b) 0.033 0.009 3.485 0.000
#> wx8 ~
#> wx7 (a) 0.060 0.009 6.641 0.000
#> wy7 (b) 0.033 0.009 3.485 0.000
#> wx9 ~
#> wx8 (a) 0.060 0.009 6.641 0.000
#> wy8 (b) 0.033 0.009 3.485 0.000
#> wx10 ~
#> wx9 (a) 0.060 0.009 6.641 0.000
#> wy9 (b) 0.033 0.009 3.485 0.000
#> wx11 ~
#> wx10 (a) 0.060 0.009 6.641 0.000
#> wy10 (b) 0.033 0.009 3.485 0.000
#> wy2 ~
#> wx1 (b) 0.033 0.009 3.485 0.000
#> wy1 (a) 0.060 0.009 6.641 0.000
#> wy3 ~
#> wx2 (b) 0.033 0.009 3.485 0.000
#> wy2 (a) 0.060 0.009 6.641 0.000
#> wy4 ~
#> wx3 (b) 0.033 0.009 3.485 0.000
#> wy3 (a) 0.060 0.009 6.641 0.000
#> wy5 ~
#> wx4 (b) 0.033 0.009 3.485 0.000
#> wy4 (a) 0.060 0.009 6.641 0.000
#> wy6 ~
#> wx5 (b) 0.033 0.009 3.485 0.000
#> wy5 (a) 0.060 0.009 6.641 0.000
#> wy7 ~
#> wx6 (b) 0.033 0.009 3.485 0.000
#> wy6 (a) 0.060 0.009 6.641 0.000
#> wy8 ~
#> wx7 (b) 0.033 0.009 3.485 0.000
#> wy7 (a) 0.060 0.009 6.641 0.000
#> wy9 ~
#> wx8 (b) 0.033 0.009 3.485 0.000
#> wy8 (a) 0.060 0.009 6.641 0.000
#> wy10 ~
#> wx9 (b) 0.033 0.009 3.485 0.000
#> wy9 (a) 0.060 0.009 6.641 0.000
#> wy11 ~
#> wx10 (b) 0.033 0.009 3.485 0.000
#> wy10 (a) 0.060 0.009 6.641 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.054 0.011 5.038 0.000
#> .wx2 ~~
#> .wy2 0.029 0.009 3.278 0.001
#> .wx3 ~~
#> .wy3 0.062 0.009 7.003 0.000
#> .wx4 ~~
#> .wy4 0.028 0.008 3.525 0.000
#> .wx5 ~~
#> .wy5 0.038 0.008 5.017 0.000
#> .wx6 ~~
#> .wy6 0.035 0.007 5.156 0.000
#> .wx7 ~~
#> .wy7 0.031 0.007 4.500 0.000
#> .wx8 ~~
#> .wy8 0.024 0.008 3.157 0.002
#> .wx9 ~~
#> .wy9 0.031 0.008 3.942 0.000
#> .wx10 ~~
#> .wy10 0.060 0.010 5.887 0.000
#> .wx11 ~~
#> .wy11 0.055 0.009 5.812 0.000
#> .RIx ~~
#> .RIy 1.116 0.045 24.683 0.000
#> .RIsx ~~
#> .RIsy 0.000 0.000 2.880 0.004
#> .RIx ~~
#> .RIsx -0.007 0.003 -2.606 0.009
#> .RIy ~~
#> .RIsy -0.011 0.003 -3.935 0.000
#> .RIx ~~
#> .RIsy -0.006 0.003 -2.150 0.032
#> .RIy ~~
#> .RIsx -0.003 0.003 -0.893 0.372
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.647 0.051 32.469 0.000
#> .RIy 1.823 0.056 32.345 0.000
#> .RIsx 0.002 0.000 6.807 0.000
#> .RIsy 0.002 0.000 7.292 0.000
#> wx1 0.285 0.014 19.984 0.000
#> wy1 0.294 0.014 20.516 0.000
#> .wx2 0.272 0.013 21.496 0.000
#> .wy2 0.224 0.011 20.538 0.000
#> .wx3 0.247 0.011 22.437 0.000
#> .wy3 0.290 0.013 23.006 0.000
#> .wx4 0.212 0.010 21.773 0.000
#> .wy4 0.237 0.011 22.066 0.000
#> .wx5 0.242 0.011 22.814 0.000
#> .wy5 0.196 0.009 22.359 0.000
#> .wx6 0.214 0.010 22.380 0.000
#> .wy6 0.179 0.008 21.978 0.000
#> .wx7 0.205 0.009 22.465 0.000
#> .wy7 0.198 0.009 22.261 0.000
#> .wx8 0.211 0.010 21.711 0.000
#> .wy8 0.217 0.010 22.304 0.000
#> .wx9 0.233 0.011 21.420 0.000
#> .wy9 0.197 0.009 21.021 0.000
#> .wx10 0.263 0.013 20.555 0.000
#> .wy10 0.250 0.012 20.312 0.000
#> .wx11 0.225 0.012 18.348 0.000
#> .wy11 0.209 0.012 17.768 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> lavaan 0.6-11 ended normally after 83 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 40
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 6137.986
#> Degrees of freedom 272
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (e) 0.282 0.002 139.133 0.000
#> RIy ~
#> oply (e) 0.282 0.002 139.133 0.000
#> RIsx ~
#> oplx (f) 0.001 0.000 4.139 0.000
#> RIsy ~
#> oply (f) 0.001 0.000 4.139 0.000
#> wx2 ~
#> wx1 (a) 0.066 0.009 7.091 0.000
#> wy1 (b) 0.009 0.010 0.933 0.351
#> wx3 ~
#> wx2 (a) 0.066 0.009 7.091 0.000
#> wy2 (b) 0.009 0.010 0.933 0.351
#> wx4 ~
#> wx3 (a) 0.066 0.009 7.091 0.000
#> wy3 (b) 0.009 0.010 0.933 0.351
#> wx5 ~
#> wx4 (a) 0.066 0.009 7.091 0.000
#> wy4 (b) 0.009 0.010 0.933 0.351
#> wx6 ~
#> wx5 (a) 0.066 0.009 7.091 0.000
#> wy5 (b) 0.009 0.010 0.933 0.351
#> wx7 ~
#> wx6 (a) 0.066 0.009 7.091 0.000
#> wy6 (b) 0.009 0.010 0.933 0.351
#> wx8 ~
#> wx7 (a) 0.066 0.009 7.091 0.000
#> wy7 (b) 0.009 0.010 0.933 0.351
#> wx9 ~
#> wx8 (a) 0.066 0.009 7.091 0.000
#> wy8 (b) 0.009 0.010 0.933 0.351
#> wx10 ~
#> wx9 (a) 0.066 0.009 7.091 0.000
#> wy9 (b) 0.009 0.010 0.933 0.351
#> wx11 ~
#> wx10 (a) 0.066 0.009 7.091 0.000
#> wy10 (b) 0.009 0.010 0.933 0.351
#> wy2 ~
#> wx1 (b) 0.009 0.010 0.933 0.351
#> wy1 (a) 0.066 0.009 7.091 0.000
#> wy3 ~
#> wx2 (b) 0.009 0.010 0.933 0.351
#> wy2 (a) 0.066 0.009 7.091 0.000
#> wy4 ~
#> wx3 (b) 0.009 0.010 0.933 0.351
#> wy3 (a) 0.066 0.009 7.091 0.000
#> wy5 ~
#> wx4 (b) 0.009 0.010 0.933 0.351
#> wy4 (a) 0.066 0.009 7.091 0.000
#> wy6 ~
#> wx5 (b) 0.009 0.010 0.933 0.351
#> wy5 (a) 0.066 0.009 7.091 0.000
#> wy7 ~
#> wx6 (b) 0.009 0.010 0.933 0.351
#> wy6 (a) 0.066 0.009 7.091 0.000
#> wy8 ~
#> wx7 (b) 0.009 0.010 0.933 0.351
#> wy7 (a) 0.066 0.009 7.091 0.000
#> wy9 ~
#> wx8 (b) 0.009 0.010 0.933 0.351
#> wy8 (a) 0.066 0.009 7.091 0.000
#> wy10 ~
#> wx9 (b) 0.009 0.010 0.933 0.351
#> wy9 (a) 0.066 0.009 7.091 0.000
#> wy11 ~
#> wx10 (b) 0.009 0.010 0.933 0.351
#> wy10 (a) 0.066 0.009 7.091 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.105 0.016 6.436 0.000
#> .wx2 ~~
#> .wy2 0.046 0.013 3.430 0.001
#> .wx3 ~~
#> .wy3 0.058 0.013 4.500 0.000
#> .wx4 ~~
#> .wy4 0.032 0.013 2.539 0.011
#> .wx5 ~~
#> .wy5 0.020 0.012 1.665 0.096
#> .wx6 ~~
#> .wy6 0.054 0.012 4.325 0.000
#> .wx7 ~~
#> .wy7 0.052 0.012 4.510 0.000
#> .wx8 ~~
#> .wy8 0.040 0.013 3.189 0.001
#> .wx9 ~~
#> .wy9 0.036 0.013 2.678 0.007
#> .wx10 ~~
#> .wy10 0.041 0.014 2.892 0.004
#> .wx11 ~~
#> .wy11 0.047 0.016 2.978 0.003
#> .RIx ~~
#> .RIy 1.042 0.046 22.479 0.000
#> .RIsx ~~
#> .RIsy 0.000 0.000 0.823 0.410
#> .RIx ~~
#> .RIsx -0.019 0.004 -5.360 0.000
#> .RIy ~~
#> .RIsy -0.021 0.004 -5.550 0.000
#> .RIx ~~
#> .RIsy -0.008 0.003 -2.453 0.014
#> .RIy ~~
#> .RIsx 0.001 0.003 0.233 0.816
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> .wx2 0.000
#> .wx3 0.000
#> .wx4 0.000
#> .wx5 0.000
#> .wx6 0.000
#> .wx7 0.000
#> .wx8 0.000
#> .wx9 0.000
#> .wx10 0.000
#> .wx11 0.000
#> wy1 0.000
#> .wy2 0.000
#> .wy3 0.000
#> .wy4 0.000
#> .wy5 0.000
#> .wy6 0.000
#> .wy7 0.000
#> .wy8 0.000
#> .wy9 0.000
#> .wy10 0.000
#> .wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.718 0.057 30.394 0.000
#> .RIy 1.656 0.057 28.874 0.000
#> .RIsx 0.002 0.000 7.151 0.000
#> .RIsy 0.002 0.000 6.694 0.000
#> wx1 0.448 0.022 20.478 0.000
#> wy1 0.432 0.021 20.173 0.000
#> .wx2 0.378 0.018 21.405 0.000
#> .wy2 0.382 0.018 21.484 0.000
#> .wx3 0.377 0.017 22.562 0.000
#> .wy3 0.396 0.018 22.493 0.000
#> .wx4 0.358 0.016 21.777 0.000
#> .wy4 0.323 0.015 21.294 0.000
#> .wx5 0.344 0.015 22.653 0.000
#> .wy5 0.354 0.016 22.753 0.000
#> .wx6 0.372 0.016 23.082 0.000
#> .wy6 0.358 0.016 22.781 0.000
#> .wx7 0.364 0.016 22.894 0.000
#> .wy7 0.306 0.014 22.140 0.000
#> .wx8 0.346 0.016 22.265 0.000
#> .wy8 0.379 0.017 22.438 0.000
#> .wx9 0.369 0.017 21.651 0.000
#> .wy9 0.369 0.017 21.490 0.000
#> .wx10 0.341 0.017 19.631 0.000
#> .wy10 0.372 0.019 19.741 0.000
#> .wx11 0.405 0.021 19.525 0.000
#> .wy11 0.349 0.019 18.242 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.0003.6.5 Summary results hypo1
| paths | est | se | pvalue | est | se | pvalue | est | se | pvalue | est | se | pvalue |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| eu-integration | ||||||||||||
| stability | 0.57 | 0.01 | 0 | 0.20 | 0.01 | 0.0 | 0.20 | 0.01 | 0.00 | 0.14 | 0.01 | 0.00 |
| partner-effect | 0.15 | 0.01 | 0 | 0.08 | 0.01 | 0.0 | 0.07 | 0.01 | 0.00 | 0.06 | 0.01 | 0.00 |
| immigrants | ||||||||||||
| stability | 0.57 | 0.00 | 0 | 0.10 | 0.01 | 0.0 | 0.10 | 0.01 | 0.00 | 0.07 | 0.01 | 0.00 |
| partner-effect | 0.16 | 0.01 | 0 | 0.03 | 0.01 | 0.0 | 0.03 | 0.01 | 0.00 | 0.01 | 0.01 | 0.12 |
| euthanasia | ||||||||||||
| stability | 0.68 | 0.00 | 0 | 0.12 | 0.01 | 0.0 | 0.11 | 0.01 | 0.00 | 0.06 | 0.01 | 0.00 |
| partner-effect | 0.18 | 0.00 | 0 | 0.04 | 0.01 | 0.0 | 0.04 | 0.01 | 0.00 | 0.03 | 0.01 | 0.00 |
| income_diff | ||||||||||||
| stability | 0.58 | 0.00 | 0 | 0.12 | 0.01 | 0.0 | 0.12 | 0.01 | 0.00 | 0.07 | 0.01 | 0.00 |
| partner-effect | 0.15 | 0.01 | 0 | 0.01 | 0.01 | 0.4 | 0.01 | 0.01 | 0.29 | 0.01 | 0.01 | 0.35 |
3.6.7 Results hypo2
Hypo2 RI-CLPM: Women are more influenced by their (male) spouse than men are influenced by their (female) spouse.
3.6.7.1 CLPM
myModel <- "
### control for education
x1 + x2 + x3 +x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 ~ ex*oplx
y1 + y2 + y3 +y4 + y5 + y6 + y7 + y8 + y9 + y10 + y11 ~ ey*oply
### Estimate the lagged effects
x2 ~ ax*x1 + bx*y1
x3 ~ ax*x2 + bx*y2
x4 ~ ax*x3 + bx*y3
x5 ~ ax*x4 + bx*y4
x6 ~ ax*x5 + bx*y5
x7 ~ ax*x6 + bx*y6
x8 ~ ax*x7 + bx*y7
x9 ~ ax*x8 + bx*y8
x10 ~ ax*x9 + bx*y9
x11 ~ ax*x10 + bx*y10
y2 ~ by*x1 + ay*y1
y3 ~ by*x2 + ay*y2
y4 ~ by*x3 + ay*y3
y5 ~ by*x4 + ay*y4
y6 ~ by*x5 + ay*y5
y7 ~ by*x6 + ay*y6
y8 ~ by*x7 + ay*y7
y9 ~ by*x8 + ay*y8
y10 ~ by*x9 + ay*y9
y11 ~ by*x10 + ay*y10
# Estimate the (residual) covariance between the variables
x1 ~~ y1 # Covariance
x2 ~~ y2
x3 ~~ y3
x4 ~~ y4
x5 ~~ y5
x6 ~~ y6
x7 ~~ y7
x8 ~~ y8
x9 ~~ y9
x10 ~~ y10
x11 ~~ y11
# Estimate the (residual) variance of the variables.
x1 ~~ x1 # Variances
y1 ~~ y1
x2 ~~ x2 # Residual variances
y2 ~~ y2
x3 ~~ x3
y3 ~~ y3
x4 ~~ x4
y4 ~~ y4
x5 ~~ x5
y5 ~~ y5
x6 ~~ x6
y6 ~~ y6
x7 ~~ x7
y7 ~~ y7
x8 ~~ x8
y8 ~~ y8
x9 ~~ x9
y9 ~~ y9
x10 ~~ x10
y10 ~~ y10
x11 ~~ x11
y11 ~~ y11
#intercepts
x1 ~ 1
y1 ~ 1
x2 ~ 1
y2 ~ 1
x3 ~ 1
y3 ~ 1
x4 ~ 1
y4 ~ 1
x5 ~ 1
y5 ~ 1
x6 ~ 1
y6 ~ 1
x7 ~ 1
y7 ~ 1
x8 ~ 1
y8 ~ 1
x9 ~ 1
y9 ~ 1
x10 ~ 1
y10 ~ 1
x11 ~ 1
y11 ~ 1
dif1 := ax - ay
dif2 := bx - by
dif3 := ex - ey
"
# Estimate models a bit faster:
estimate <- function(x) lavaan(myModel, data = x, missing = "fiml.x", meanstructure = T)
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
summary(results_temp[[1]])
results[[17]] <- results_temp[[1]]
results[[18]] <- results_temp[[2]]
results[[19]] <- results_temp[[3]]
results[[20]] <- results_temp[[4]]
names(results)[17:20] <- c("fitm1h2y1", "fitm1h2y2", "fitm1h2y3", "fitm1h2y4")load("addfiles/results.Rdata")
summary(results[[17]])
summary(results[[18]])
summary(results[[19]])
summary(results[[20]])#> lavaan 0.6-11 ended normally after 39 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 56
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 3233.567
#> Degrees of freedom 258
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x2 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x3 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x4 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x5 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x6 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x7 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x8 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x9 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x10 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> x11 ~
#> oplx (ex) 0.043 0.002 17.477 0.000
#> y1 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y2 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y3 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y4 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y5 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y6 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y7 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y8 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y9 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y10 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> y11 ~
#> oply (ey) 0.036 0.002 15.163 0.000
#> x2 ~
#> x1 (ax) 0.605 0.007 86.610 0.000
#> y1 (bx) 0.163 0.009 18.854 0.000
#> x3 ~
#> x2 (ax) 0.605 0.007 86.610 0.000
#> y2 (bx) 0.163 0.009 18.854 0.000
#> x4 ~
#> x3 (ax) 0.605 0.007 86.610 0.000
#> y3 (bx) 0.163 0.009 18.854 0.000
#> x5 ~
#> x4 (ax) 0.605 0.007 86.610 0.000
#> y4 (bx) 0.163 0.009 18.854 0.000
#> x6 ~
#> x5 (ax) 0.605 0.007 86.610 0.000
#> y5 (bx) 0.163 0.009 18.854 0.000
#> x7 ~
#> x6 (ax) 0.605 0.007 86.610 0.000
#> y6 (bx) 0.163 0.009 18.854 0.000
#> x8 ~
#> x7 (ax) 0.605 0.007 86.610 0.000
#> y7 (bx) 0.163 0.009 18.854 0.000
#> x9 ~
#> x8 (ax) 0.605 0.007 86.610 0.000
#> y8 (bx) 0.163 0.009 18.854 0.000
#> x10 ~
#> x9 (ax) 0.605 0.007 86.610 0.000
#> y9 (bx) 0.163 0.009 18.854 0.000
#> x11 ~
#> x10 (ax) 0.605 0.007 86.610 0.000
#> y10 (bx) 0.163 0.009 18.854 0.000
#> y2 ~
#> x1 (by) 0.151 0.007 23.192 0.000
#> y1 (ay) 0.525 0.008 67.181 0.000
#> y3 ~
#> x2 (by) 0.151 0.007 23.192 0.000
#> y2 (ay) 0.525 0.008 67.181 0.000
#> y4 ~
#> x3 (by) 0.151 0.007 23.192 0.000
#> y3 (ay) 0.525 0.008 67.181 0.000
#> y5 ~
#> x4 (by) 0.151 0.007 23.192 0.000
#> y4 (ay) 0.525 0.008 67.181 0.000
#> y6 ~
#> x5 (by) 0.151 0.007 23.192 0.000
#> y5 (ay) 0.525 0.008 67.181 0.000
#> y7 ~
#> x6 (by) 0.151 0.007 23.192 0.000
#> y6 (ay) 0.525 0.008 67.181 0.000
#> y8 ~
#> x7 (by) 0.151 0.007 23.192 0.000
#> y7 (ay) 0.525 0.008 67.181 0.000
#> y9 ~
#> x8 (by) 0.151 0.007 23.192 0.000
#> y8 (ay) 0.525 0.008 67.181 0.000
#> y10 ~
#> x9 (by) 0.151 0.007 23.192 0.000
#> y9 (ay) 0.525 0.008 67.181 0.000
#> y11 ~
#> x10 (by) 0.151 0.007 23.192 0.000
#> y10 (ay) 0.525 0.008 67.181 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.410 0.030 13.668 0.000
#> .x2 ~~
#> .y2 0.123 0.021 5.822 0.000
#> .x3 ~~
#> .y3 0.119 0.020 5.841 0.000
#> .x4 ~~
#> .y4 0.154 0.022 7.146 0.000
#> .x5 ~~
#> .y5 0.146 0.025 5.956 0.000
#> .x6 ~~
#> .y6 0.112 0.020 5.655 0.000
#> .x7 ~~
#> .y7 0.104 0.018 5.963 0.000
#> .x8 ~~
#> .y8 0.114 0.021 5.336 0.000
#> .x9 ~~
#> .y9 0.119 0.022 5.476 0.000
#> .x10 ~~
#> .y10 0.081 0.023 3.487 0.000
#> .x11 ~~
#> .y11 0.131 0.024 5.568 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.087 0.040 27.297 0.000
#> .y1 1.125 0.036 31.131 0.000
#> .x2 -0.030 0.037 -0.818 0.413
#> .y2 0.179 0.034 5.266 0.000
#> .x3 -0.107 0.037 -2.916 0.004
#> .y3 0.118 0.034 3.499 0.000
#> .x4 -0.408 0.038 -10.870 0.000
#> .y4 -0.216 0.034 -6.268 0.000
#> .x5 -0.001 0.038 -0.039 0.969
#> .y5 0.015 0.035 0.418 0.676
#> .x6 -0.304 0.036 -8.390 0.000
#> .y6 -0.054 0.034 -1.600 0.110
#> .x7 -0.295 0.036 -8.238 0.000
#> .y7 -0.089 0.033 -2.666 0.008
#> .x8 -0.124 0.037 -3.329 0.001
#> .y8 0.062 0.035 1.785 0.074
#> .x9 -0.278 0.037 -7.464 0.000
#> .y9 -0.013 0.035 -0.376 0.707
#> .x10 -0.067 0.038 -1.745 0.081
#> .y10 0.177 0.036 4.925 0.000
#> .x11 -0.083 0.039 -2.115 0.034
#> .y11 0.137 0.036 3.769 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.375 0.045 30.425 0.000
#> .y1 1.013 0.034 29.369 0.000
#> .x2 0.825 0.030 27.054 0.000
#> .y2 0.679 0.026 26.286 0.000
#> .x3 0.775 0.029 26.359 0.000
#> .y3 0.599 0.024 25.470 0.000
#> .x4 0.809 0.031 25.775 0.000
#> .y4 0.642 0.026 24.959 0.000
#> .x5 0.922 0.036 25.674 0.000
#> .y5 0.703 0.028 25.034 0.000
#> .x6 0.703 0.027 25.881 0.000
#> .y6 0.584 0.023 24.937 0.000
#> .x7 0.637 0.025 25.650 0.000
#> .y7 0.532 0.021 24.981 0.000
#> .x8 0.741 0.029 25.230 0.000
#> .y8 0.628 0.025 24.978 0.000
#> .x9 0.744 0.029 25.613 0.000
#> .y9 0.648 0.026 24.738 0.000
#> .x10 0.757 0.031 24.217 0.000
#> .y10 0.651 0.028 23.538 0.000
#> .x11 0.787 0.033 23.979 0.000
#> .y11 0.625 0.027 22.882 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.080 0.011 7.385 0.000
#> dif2 0.012 0.011 1.097 0.273
#> dif3 0.007 0.003 2.106 0.035
#>
#> lavaan 0.6-11 ended normally after 38 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 56
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 4304.782
#> Degrees of freedom 258
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x2 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x3 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x4 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x5 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x6 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x7 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x8 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x9 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x10 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> x11 ~
#> oplx (ex) 0.024 0.002 12.493 0.000
#> y1 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y2 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y3 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y4 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y5 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y6 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y7 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y8 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y9 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y10 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> y11 ~
#> oply (ey) 0.029 0.002 14.613 0.000
#> x2 ~
#> x1 (ax) 0.569 0.007 79.995 0.000
#> y1 (bx) 0.176 0.007 23.736 0.000
#> x3 ~
#> x2 (ax) 0.569 0.007 79.995 0.000
#> y2 (bx) 0.176 0.007 23.736 0.000
#> x4 ~
#> x3 (ax) 0.569 0.007 79.995 0.000
#> y3 (bx) 0.176 0.007 23.736 0.000
#> x5 ~
#> x4 (ax) 0.569 0.007 79.995 0.000
#> y4 (bx) 0.176 0.007 23.736 0.000
#> x6 ~
#> x5 (ax) 0.569 0.007 79.995 0.000
#> y5 (bx) 0.176 0.007 23.736 0.000
#> x7 ~
#> x6 (ax) 0.569 0.007 79.995 0.000
#> y6 (bx) 0.176 0.007 23.736 0.000
#> x8 ~
#> x7 (ax) 0.569 0.007 79.995 0.000
#> y7 (bx) 0.176 0.007 23.736 0.000
#> x9 ~
#> x8 (ax) 0.569 0.007 79.995 0.000
#> y8 (bx) 0.176 0.007 23.736 0.000
#> x10 ~
#> x9 (ax) 0.569 0.007 79.995 0.000
#> y9 (bx) 0.176 0.007 23.736 0.000
#> x11 ~
#> x10 (ax) 0.569 0.007 79.995 0.000
#> y10 (bx) 0.176 0.007 23.736 0.000
#> y2 ~
#> x1 (by) 0.152 0.007 21.425 0.000
#> y1 (ay) 0.572 0.007 79.358 0.000
#> y3 ~
#> x2 (by) 0.152 0.007 21.425 0.000
#> y2 (ay) 0.572 0.007 79.358 0.000
#> y4 ~
#> x3 (by) 0.152 0.007 21.425 0.000
#> y3 (ay) 0.572 0.007 79.358 0.000
#> y5 ~
#> x4 (by) 0.152 0.007 21.425 0.000
#> y4 (ay) 0.572 0.007 79.358 0.000
#> y6 ~
#> x5 (by) 0.152 0.007 21.425 0.000
#> y5 (ay) 0.572 0.007 79.358 0.000
#> y7 ~
#> x6 (by) 0.152 0.007 21.425 0.000
#> y6 (ay) 0.572 0.007 79.358 0.000
#> y8 ~
#> x7 (by) 0.152 0.007 21.425 0.000
#> y7 (ay) 0.572 0.007 79.358 0.000
#> y9 ~
#> x8 (by) 0.152 0.007 21.425 0.000
#> y8 (ay) 0.572 0.007 79.358 0.000
#> y10 ~
#> x9 (by) 0.152 0.007 21.425 0.000
#> y9 (ay) 0.572 0.007 79.358 0.000
#> y11 ~
#> x10 (by) 0.152 0.007 21.425 0.000
#> y10 (ay) 0.572 0.007 79.358 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.383 0.023 16.611 0.000
#> .x2 ~~
#> .y2 0.101 0.015 6.608 0.000
#> .x3 ~~
#> .y3 0.104 0.015 6.808 0.000
#> .x4 ~~
#> .y4 0.071 0.014 5.063 0.000
#> .x5 ~~
#> .y5 0.086 0.014 6.086 0.000
#> .x6 ~~
#> .y6 0.073 0.014 5.334 0.000
#> .x7 ~~
#> .y7 0.055 0.014 4.040 0.000
#> .x8 ~~
#> .y8 0.075 0.015 5.110 0.000
#> .x9 ~~
#> .y9 0.041 0.015 2.712 0.007
#> .x10 ~~
#> .y10 0.089 0.015 5.882 0.000
#> .x11 ~~
#> .y11 0.101 0.015 6.750 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.917 0.032 28.541 0.000
#> .y1 0.927 0.031 30.028 0.000
#> .x2 0.038 0.030 1.266 0.206
#> .y2 0.043 0.029 1.499 0.134
#> .x3 0.009 0.030 0.313 0.754
#> .y3 0.054 0.029 1.898 0.058
#> .x4 0.010 0.029 0.330 0.741
#> .y4 0.025 0.029 0.873 0.382
#> .x5 0.008 0.030 0.266 0.790
#> .y5 0.025 0.029 0.871 0.384
#> .x6 0.007 0.030 0.222 0.825
#> .y6 0.025 0.028 0.893 0.372
#> .x7 0.029 0.030 0.976 0.329
#> .y7 0.050 0.028 1.765 0.078
#> .x8 -0.036 0.030 -1.210 0.226
#> .y8 -0.012 0.029 -0.406 0.685
#> .x9 -0.046 0.030 -1.500 0.134
#> .y9 0.004 0.030 0.124 0.902
#> .x10 0.115 0.031 3.711 0.000
#> .y10 0.112 0.030 3.768 0.000
#> .x11 0.001 0.031 0.017 0.986
#> .y11 0.039 0.030 1.313 0.189
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.946 0.031 30.278 0.000
#> .y1 0.869 0.029 30.124 0.000
#> .x2 0.567 0.021 27.152 0.000
#> .y2 0.551 0.020 27.172 0.000
#> .x3 0.548 0.021 26.509 0.000
#> .y3 0.504 0.019 26.222 0.000
#> .x4 0.460 0.018 25.860 0.000
#> .y4 0.485 0.019 25.470 0.000
#> .x5 0.477 0.019 25.760 0.000
#> .y5 0.463 0.018 25.114 0.000
#> .x6 0.505 0.019 26.222 0.000
#> .y6 0.442 0.017 26.327 0.000
#> .x7 0.488 0.019 25.910 0.000
#> .y7 0.451 0.017 26.076 0.000
#> .x8 0.479 0.019 25.427 0.000
#> .y8 0.484 0.019 25.571 0.000
#> .x9 0.501 0.019 25.754 0.000
#> .y9 0.506 0.020 25.472 0.000
#> .x10 0.511 0.021 24.631 0.000
#> .y10 0.454 0.019 24.284 0.000
#> .x11 0.492 0.020 24.422 0.000
#> .y11 0.451 0.019 24.049 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.003 0.010 -0.301 0.763
#> dif2 0.024 0.010 2.265 0.024
#> dif3 -0.004 0.003 -1.575 0.115
#>
#> lavaan 0.6-11 ended normally after 68 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 56
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5137.978
#> Degrees of freedom 258
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x2 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x3 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x4 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x5 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x6 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x7 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x8 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x9 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x10 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> x11 ~
#> oplx (ex) 0.004 0.002 2.542 0.011
#> y1 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y2 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y3 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y4 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y5 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y6 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y7 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y8 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y9 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y10 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> y11 ~
#> oply (ey) 0.004 0.002 2.244 0.025
#> x2 ~
#> x1 (ax) 0.663 0.007 101.002 0.000
#> y1 (bx) 0.192 0.007 29.543 0.000
#> x3 ~
#> x2 (ax) 0.663 0.007 101.002 0.000
#> y2 (bx) 0.192 0.007 29.543 0.000
#> x4 ~
#> x3 (ax) 0.663 0.007 101.002 0.000
#> y3 (bx) 0.192 0.007 29.543 0.000
#> x5 ~
#> x4 (ax) 0.663 0.007 101.002 0.000
#> y4 (bx) 0.192 0.007 29.543 0.000
#> x6 ~
#> x5 (ax) 0.663 0.007 101.002 0.000
#> y5 (bx) 0.192 0.007 29.543 0.000
#> x7 ~
#> x6 (ax) 0.663 0.007 101.002 0.000
#> y6 (bx) 0.192 0.007 29.543 0.000
#> x8 ~
#> x7 (ax) 0.663 0.007 101.002 0.000
#> y7 (bx) 0.192 0.007 29.543 0.000
#> x9 ~
#> x8 (ax) 0.663 0.007 101.002 0.000
#> y8 (bx) 0.192 0.007 29.543 0.000
#> x10 ~
#> x9 (ax) 0.663 0.007 101.002 0.000
#> y9 (bx) 0.192 0.007 29.543 0.000
#> x11 ~
#> x10 (ax) 0.663 0.007 101.002 0.000
#> y10 (bx) 0.192 0.007 29.543 0.000
#> y2 ~
#> x1 (by) 0.172 0.007 25.776 0.000
#> y1 (ay) 0.697 0.006 109.007 0.000
#> y3 ~
#> x2 (by) 0.172 0.007 25.776 0.000
#> y2 (ay) 0.697 0.006 109.007 0.000
#> y4 ~
#> x3 (by) 0.172 0.007 25.776 0.000
#> y3 (ay) 0.697 0.006 109.007 0.000
#> y5 ~
#> x4 (by) 0.172 0.007 25.776 0.000
#> y4 (ay) 0.697 0.006 109.007 0.000
#> y6 ~
#> x5 (by) 0.172 0.007 25.776 0.000
#> y5 (ay) 0.697 0.006 109.007 0.000
#> y7 ~
#> x6 (by) 0.172 0.007 25.776 0.000
#> y6 (ay) 0.697 0.006 109.007 0.000
#> y8 ~
#> x7 (by) 0.172 0.007 25.776 0.000
#> y7 (ay) 0.697 0.006 109.007 0.000
#> y9 ~
#> x8 (by) 0.172 0.007 25.776 0.000
#> y8 (ay) 0.697 0.006 109.007 0.000
#> y10 ~
#> x9 (by) 0.172 0.007 25.776 0.000
#> y9 (ay) 0.697 0.006 109.007 0.000
#> y11 ~
#> x10 (by) 0.172 0.007 25.776 0.000
#> y10 (ay) 0.697 0.006 109.007 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.659 0.029 22.944 0.000
#> .x2 ~~
#> .y2 0.081 0.012 6.888 0.000
#> .x3 ~~
#> .y3 0.086 0.011 7.794 0.000
#> .x4 ~~
#> .y4 0.086 0.011 7.827 0.000
#> .x5 ~~
#> .y5 0.078 0.010 7.479 0.000
#> .x6 ~~
#> .y6 0.066 0.009 7.415 0.000
#> .x7 ~~
#> .y7 0.056 0.009 6.178 0.000
#> .x8 ~~
#> .y8 0.062 0.010 6.021 0.000
#> .x9 ~~
#> .y9 0.075 0.011 7.104 0.000
#> .x10 ~~
#> .y10 0.096 0.013 7.549 0.000
#> .x11 ~~
#> .y11 0.101 0.012 8.429 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 4.254 0.029 144.503 0.000
#> .y1 4.277 0.029 145.918 0.000
#> .x2 0.588 0.033 17.686 0.000
#> .y2 0.563 0.032 17.659 0.000
#> .x3 0.566 0.033 17.314 0.000
#> .y3 0.505 0.032 15.659 0.000
#> .x4 0.608 0.033 18.669 0.000
#> .y4 0.576 0.032 17.810 0.000
#> .x5 0.596 0.033 18.115 0.000
#> .y5 0.556 0.032 17.357 0.000
#> .x6 0.599 0.033 18.210 0.000
#> .y6 0.547 0.031 17.557 0.000
#> .x7 0.617 0.033 18.895 0.000
#> .y7 0.562 0.032 17.722 0.000
#> .x8 0.600 0.033 18.089 0.000
#> .y8 0.551 0.033 16.924 0.000
#> .x9 0.539 0.034 16.020 0.000
#> .y9 0.510 0.032 15.819 0.000
#> .x10 0.572 0.034 16.738 0.000
#> .y10 0.519 0.033 15.711 0.000
#> .x11 0.627 0.034 18.473 0.000
#> .y11 0.575 0.033 17.293 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.062 0.034 31.012 0.000
#> .y1 1.112 0.036 30.945 0.000
#> .x2 0.440 0.016 26.796 0.000
#> .y2 0.392 0.015 26.698 0.000
#> .x3 0.361 0.014 26.107 0.000
#> .y3 0.406 0.016 25.958 0.000
#> .x4 0.339 0.013 26.022 0.000
#> .y4 0.402 0.016 25.847 0.000
#> .x5 0.340 0.013 25.598 0.000
#> .y5 0.346 0.014 25.297 0.000
#> .x6 0.344 0.013 26.425 0.000
#> .y6 0.271 0.011 25.766 0.000
#> .x7 0.308 0.012 25.913 0.000
#> .y7 0.306 0.012 25.227 0.000
#> .x8 0.325 0.013 25.062 0.000
#> .y8 0.349 0.014 24.754 0.000
#> .x9 0.369 0.015 25.268 0.000
#> .y9 0.320 0.013 25.193 0.000
#> .x10 0.395 0.017 23.634 0.000
#> .y10 0.358 0.015 23.933 0.000
#> .x11 0.362 0.015 24.042 0.000
#> .y11 0.367 0.015 23.806 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.034 0.010 -3.489 0.000
#> dif2 0.020 0.010 2.051 0.040
#> dif3 0.000 0.002 0.218 0.827
#>
#> lavaan 0.6-11 ended normally after 54 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 117
#> Number of equality constraints 56
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 4146.492
#> Degrees of freedom 258
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> x1 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x2 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x3 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x4 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x5 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x6 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x7 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x8 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x9 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x10 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> x11 ~
#> oplx (ex) -0.020 0.002 -10.112 0.000
#> y1 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y2 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y3 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y4 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y5 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y6 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y7 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y8 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y9 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y10 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> y11 ~
#> oply (ey) -0.014 0.002 -6.762 0.000
#> x2 ~
#> x1 (ax) 0.606 0.007 87.759 0.000
#> y1 (bx) 0.143 0.008 18.295 0.000
#> x3 ~
#> x2 (ax) 0.606 0.007 87.759 0.000
#> y2 (bx) 0.143 0.008 18.295 0.000
#> x4 ~
#> x3 (ax) 0.606 0.007 87.759 0.000
#> y3 (bx) 0.143 0.008 18.295 0.000
#> x5 ~
#> x4 (ax) 0.606 0.007 87.759 0.000
#> y4 (bx) 0.143 0.008 18.295 0.000
#> x6 ~
#> x5 (ax) 0.606 0.007 87.759 0.000
#> y5 (bx) 0.143 0.008 18.295 0.000
#> x7 ~
#> x6 (ax) 0.606 0.007 87.759 0.000
#> y6 (bx) 0.143 0.008 18.295 0.000
#> x8 ~
#> x7 (ax) 0.606 0.007 87.759 0.000
#> y7 (bx) 0.143 0.008 18.295 0.000
#> x9 ~
#> x8 (ax) 0.606 0.007 87.759 0.000
#> y8 (bx) 0.143 0.008 18.295 0.000
#> x10 ~
#> x9 (ax) 0.606 0.007 87.759 0.000
#> y9 (bx) 0.143 0.008 18.295 0.000
#> x11 ~
#> x10 (ax) 0.606 0.007 87.759 0.000
#> y10 (bx) 0.143 0.008 18.295 0.000
#> y2 ~
#> x1 (by) 0.152 0.007 21.574 0.000
#> y1 (ay) 0.539 0.008 71.026 0.000
#> y3 ~
#> x2 (by) 0.152 0.007 21.574 0.000
#> y2 (ay) 0.539 0.008 71.026 0.000
#> y4 ~
#> x3 (by) 0.152 0.007 21.574 0.000
#> y3 (ay) 0.539 0.008 71.026 0.000
#> y5 ~
#> x4 (by) 0.152 0.007 21.574 0.000
#> y4 (ay) 0.539 0.008 71.026 0.000
#> y6 ~
#> x5 (by) 0.152 0.007 21.574 0.000
#> y5 (ay) 0.539 0.008 71.026 0.000
#> y7 ~
#> x6 (by) 0.152 0.007 21.574 0.000
#> y6 (ay) 0.539 0.008 71.026 0.000
#> y8 ~
#> x7 (by) 0.152 0.007 21.574 0.000
#> y7 (ay) 0.539 0.008 71.026 0.000
#> y9 ~
#> x8 (by) 0.152 0.007 21.574 0.000
#> y8 (ay) 0.539 0.008 71.026 0.000
#> y10 ~
#> x9 (by) 0.152 0.007 21.574 0.000
#> y9 (ay) 0.539 0.008 71.026 0.000
#> y11 ~
#> x10 (by) 0.152 0.007 21.574 0.000
#> y10 (ay) 0.539 0.008 71.026 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 ~~
#> .y1 0.421 0.025 16.634 0.000
#> .x2 ~~
#> .y2 0.140 0.016 8.814 0.000
#> .x3 ~~
#> .y3 0.099 0.016 6.276 0.000
#> .x4 ~~
#> .y4 0.111 0.017 6.581 0.000
#> .x5 ~~
#> .y5 0.064 0.014 4.462 0.000
#> .x6 ~~
#> .y6 0.133 0.016 8.390 0.000
#> .x7 ~~
#> .y7 0.091 0.014 6.399 0.000
#> .x8 ~~
#> .y8 0.085 0.016 5.396 0.000
#> .x9 ~~
#> .y9 0.102 0.017 6.129 0.000
#> .x10 ~~
#> .y10 0.093 0.017 5.451 0.000
#> .x11 ~~
#> .y11 0.071 0.017 4.076 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 3.891 0.034 115.721 0.000
#> .y1 3.968 0.032 123.603 0.000
#> .x2 1.174 0.045 26.127 0.000
#> .y2 1.431 0.043 33.089 0.000
#> .x3 1.144 0.045 25.458 0.000
#> .y3 1.332 0.044 30.327 0.000
#> .x4 1.145 0.045 25.352 0.000
#> .y4 1.375 0.044 31.356 0.000
#> .x5 1.262 0.045 28.302 0.000
#> .y5 1.425 0.043 32.801 0.000
#> .x6 1.065 0.046 23.342 0.000
#> .y6 1.296 0.044 29.325 0.000
#> .x7 1.163 0.045 26.035 0.000
#> .y7 1.349 0.043 31.216 0.000
#> .x8 1.211 0.045 26.754 0.000
#> .y8 1.402 0.044 31.804 0.000
#> .x9 1.196 0.046 26.224 0.000
#> .y9 1.366 0.045 30.539 0.000
#> .x10 1.185 0.046 25.819 0.000
#> .y10 1.332 0.045 29.538 0.000
#> .x11 1.237 0.046 26.737 0.000
#> .y11 1.361 0.045 30.067 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.090 0.036 30.464 0.000
#> .y1 0.914 0.030 30.174 0.000
#> .x2 0.606 0.022 27.077 0.000
#> .y2 0.539 0.020 27.048 0.000
#> .x3 0.536 0.020 26.341 0.000
#> .y3 0.559 0.021 26.210 0.000
#> .x4 0.560 0.022 25.830 0.000
#> .y4 0.534 0.021 25.457 0.000
#> .x5 0.463 0.018 25.301 0.000
#> .y5 0.479 0.019 25.243 0.000
#> .x6 0.555 0.021 26.217 0.000
#> .y6 0.534 0.020 26.107 0.000
#> .x7 0.495 0.019 26.004 0.000
#> .y7 0.447 0.017 25.646 0.000
#> .x8 0.532 0.021 25.615 0.000
#> .y8 0.508 0.020 25.372 0.000
#> .x9 0.548 0.021 25.808 0.000
#> .y9 0.542 0.022 25.161 0.000
#> .x10 0.529 0.022 24.542 0.000
#> .y10 0.533 0.022 24.184 0.000
#> .x11 0.543 0.022 24.296 0.000
#> .y11 0.522 0.022 23.746 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.067 0.011 6.294 0.000
#> dif2 -0.009 0.011 -0.803 0.422
#> dif3 -0.006 0.003 -2.275 0.0233.6.7.2 RI-CLPM
RICLPM <- '
# Create between components (random intercepts)
RIx =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11
RIy =~ 1*y1 + 1*y2 + 1*y3 + 1*y4 + 1*y5 + 1*y6 + 1*y7 + 1*y8 + 1*y9 + 1*y10 + 1*y11
RIx ~ ex*oplx
RIy ~ ey*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
x2 ~ ax*x1 + bx*y1
x3 ~ ax*x2 + bx*y2
x4 ~ ax*x3 + bx*y3
x5 ~ ax*x4 + bx*y4
x6 ~ ax*x5 + bx*y5
x7 ~ ax*x6 + bx*y6
x8 ~ ax*x7 + bx*y7
x9 ~ ax*x8 + bx*y8
x10 ~ ax*x9 + bx*y9
x11 ~ ax*x10 + bx*y10
y2 ~ by*x1 + ay*y1
y3 ~ by*x2 + ay*y2
y4 ~ by*x3 + ay*y3
y5 ~ by*x4 + ay*y4
y6 ~ by*x5 + ay*y5
y7 ~ by*x6 + ay*y6
y8 ~ by*x7 + ay*y7
y9 ~ by*x8 + ay*y8
y10 ~ by*x9 + ay*y9
y11 ~ by*x10 + ay*y10
dif1 := ax - ay
dif2 := bx - by
dif3 := ex - ey
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(RICLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
summary(results_temp[[4]])
results[[21]] <- results_temp[[1]]
results[[22]] <- results_temp[[2]]
results[[23]] <- results_temp[[3]]
results[[24]] <- results_temp[[4]]
names(results)[21:24] <- c("fitm2h2y1", "fitm2h2y2","fitm2h2y3","fitm2h2y4")
save(results, file="results.RData")load("addfiles/results.Rdata")
summary(results[[21]])
summary(results[[22]])
summary(results[[23]])
summary(results[[24]])#> lavaan 0.6-11 ended normally after 32 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1997.479
#> Degrees of freedom 277
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.107 0.002 62.193 0.000
#> RIy ~
#> oply (ey) 0.108 0.002 66.277 0.000
#> x2 ~
#> x1 (ax) 0.131 0.010 13.320 0.000
#> y1 (bx) 0.004 0.011 0.423 0.672
#> x3 ~
#> x2 (ax) 0.131 0.010 13.320 0.000
#> y2 (bx) 0.004 0.011 0.423 0.672
#> x4 ~
#> x3 (ax) 0.131 0.010 13.320 0.000
#> y3 (bx) 0.004 0.011 0.423 0.672
#> x5 ~
#> x4 (ax) 0.131 0.010 13.320 0.000
#> y4 (bx) 0.004 0.011 0.423 0.672
#> x6 ~
#> x5 (ax) 0.131 0.010 13.320 0.000
#> y5 (bx) 0.004 0.011 0.423 0.672
#> x7 ~
#> x6 (ax) 0.131 0.010 13.320 0.000
#> y6 (bx) 0.004 0.011 0.423 0.672
#> x8 ~
#> x7 (ax) 0.131 0.010 13.320 0.000
#> y7 (bx) 0.004 0.011 0.423 0.672
#> x9 ~
#> x8 (ax) 0.131 0.010 13.320 0.000
#> y8 (bx) 0.004 0.011 0.423 0.672
#> x10 ~
#> x9 (ax) 0.131 0.010 13.320 0.000
#> y9 (bx) 0.004 0.011 0.423 0.672
#> x11 ~
#> x10 (ax) 0.131 0.010 13.320 0.000
#> y10 (bx) 0.004 0.011 0.423 0.672
#> y2 ~
#> x1 (by) 0.029 0.009 3.263 0.001
#> y1 (ay) 0.100 0.010 9.719 0.000
#> y3 ~
#> x2 (by) 0.029 0.009 3.263 0.001
#> y2 (ay) 0.100 0.010 9.719 0.000
#> y4 ~
#> x3 (by) 0.029 0.009 3.263 0.001
#> y3 (ay) 0.100 0.010 9.719 0.000
#> y5 ~
#> x4 (by) 0.029 0.009 3.263 0.001
#> y4 (ay) 0.100 0.010 9.719 0.000
#> y6 ~
#> x5 (by) 0.029 0.009 3.263 0.001
#> y5 (ay) 0.100 0.010 9.719 0.000
#> y7 ~
#> x6 (by) 0.029 0.009 3.263 0.001
#> y6 (ay) 0.100 0.010 9.719 0.000
#> y8 ~
#> x7 (by) 0.029 0.009 3.263 0.001
#> y7 (ay) 0.100 0.010 9.719 0.000
#> y9 ~
#> x8 (by) 0.029 0.009 3.263 0.001
#> y8 (ay) 0.100 0.010 9.719 0.000
#> y10 ~
#> x9 (by) 0.029 0.009 3.263 0.001
#> y9 (ay) 0.100 0.010 9.719 0.000
#> y11 ~
#> x10 (by) 0.029 0.009 3.263 0.001
#> y10 (ay) 0.100 0.010 9.719 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.208 0.026 8.085 0.000
#> wx2 ~~
#> wy2 0.109 0.020 5.432 0.000
#> wx3 ~~
#> wy3 0.136 0.019 7.010 0.000
#> wx4 ~~
#> wy4 0.092 0.018 5.055 0.000
#> wx5 ~~
#> wy5 0.087 0.021 4.158 0.000
#> wx6 ~~
#> wy6 0.057 0.016 3.567 0.000
#> wx7 ~~
#> wy7 0.094 0.016 5.990 0.000
#> wx8 ~~
#> wy8 0.074 0.018 4.163 0.000
#> wx9 ~~
#> wy9 0.096 0.019 5.030 0.000
#> wx10 ~~
#> wy10 0.032 0.020 1.629 0.103
#> wx11 ~~
#> wy11 0.101 0.021 4.810 0.000
#> .RIx ~~
#> .RIy 0.285 0.016 18.369 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.610 0.024 25.889 0.000
#> .RIy 0.411 0.017 23.879 0.000
#> wx1 0.831 0.036 23.057 0.000
#> wy1 0.706 0.031 22.464 0.000
#> wx2 0.702 0.029 23.981 0.000
#> wy2 0.567 0.024 23.148 0.000
#> wx3 0.623 0.026 23.779 0.000
#> wy3 0.542 0.024 22.994 0.000
#> wx4 0.577 0.026 22.451 0.000
#> wy4 0.463 0.021 21.622 0.000
#> wx5 0.732 0.030 24.014 0.000
#> wy5 0.546 0.024 23.234 0.000
#> wx6 0.494 0.022 22.803 0.000
#> wy6 0.410 0.019 21.986 0.000
#> wx7 0.476 0.021 22.625 0.000
#> wy7 0.438 0.020 22.399 0.000
#> wx8 0.529 0.023 22.915 0.000
#> wy8 0.490 0.022 22.687 0.000
#> wx9 0.600 0.026 22.936 0.000
#> wy9 0.493 0.022 21.983 0.000
#> wx10 0.545 0.025 21.594 0.000
#> wy10 0.490 0.023 21.146 0.000
#> wx11 0.604 0.028 21.355 0.000
#> wy11 0.523 0.026 20.465 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.031 0.014 2.157 0.031
#> dif2 -0.025 0.013 -1.817 0.069
#> dif3 -0.000 0.002 -0.137 0.891
#>
#> lavaan 0.6-11 ended normally after 41 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 802.295
#> Degrees of freedom 277
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.092 0.001 67.348 0.000
#> RIy ~
#> oply (ey) 0.102 0.001 74.487 0.000
#> x2 ~
#> x1 (ax) 0.064 0.009 7.024 0.000
#> y1 (bx) 0.027 0.009 2.946 0.003
#> x3 ~
#> x2 (ax) 0.064 0.009 7.024 0.000
#> y2 (bx) 0.027 0.009 2.946 0.003
#> x4 ~
#> x3 (ax) 0.064 0.009 7.024 0.000
#> y3 (bx) 0.027 0.009 2.946 0.003
#> x5 ~
#> x4 (ax) 0.064 0.009 7.024 0.000
#> y4 (bx) 0.027 0.009 2.946 0.003
#> x6 ~
#> x5 (ax) 0.064 0.009 7.024 0.000
#> y5 (bx) 0.027 0.009 2.946 0.003
#> x7 ~
#> x6 (ax) 0.064 0.009 7.024 0.000
#> y6 (bx) 0.027 0.009 2.946 0.003
#> x8 ~
#> x7 (ax) 0.064 0.009 7.024 0.000
#> y7 (bx) 0.027 0.009 2.946 0.003
#> x9 ~
#> x8 (ax) 0.064 0.009 7.024 0.000
#> y8 (bx) 0.027 0.009 2.946 0.003
#> x10 ~
#> x9 (ax) 0.064 0.009 7.024 0.000
#> y9 (bx) 0.027 0.009 2.946 0.003
#> x11 ~
#> x10 (ax) 0.064 0.009 7.024 0.000
#> y10 (bx) 0.027 0.009 2.946 0.003
#> y2 ~
#> x1 (by) 0.010 0.009 1.125 0.261
#> y1 (ay) 0.065 0.009 7.188 0.000
#> y3 ~
#> x2 (by) 0.010 0.009 1.125 0.261
#> y2 (ay) 0.065 0.009 7.188 0.000
#> y4 ~
#> x3 (by) 0.010 0.009 1.125 0.261
#> y3 (ay) 0.065 0.009 7.188 0.000
#> y5 ~
#> x4 (by) 0.010 0.009 1.125 0.261
#> y4 (ay) 0.065 0.009 7.188 0.000
#> y6 ~
#> x5 (by) 0.010 0.009 1.125 0.261
#> y5 (ay) 0.065 0.009 7.188 0.000
#> y7 ~
#> x6 (by) 0.010 0.009 1.125 0.261
#> y6 (ay) 0.065 0.009 7.188 0.000
#> y8 ~
#> x7 (by) 0.010 0.009 1.125 0.261
#> y7 (ay) 0.065 0.009 7.188 0.000
#> y9 ~
#> x8 (by) 0.010 0.009 1.125 0.261
#> y8 (ay) 0.065 0.009 7.188 0.000
#> y10 ~
#> x9 (by) 0.010 0.009 1.125 0.261
#> y9 (ay) 0.065 0.009 7.188 0.000
#> y11 ~
#> x10 (by) 0.010 0.009 1.125 0.261
#> y10 (ay) 0.065 0.009 7.188 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.063 0.013 4.778 0.000
#> wx2 ~~
#> wy2 0.045 0.013 3.552 0.000
#> wx3 ~~
#> wy3 0.027 0.011 2.439 0.015
#> wx4 ~~
#> wy4 0.043 0.011 3.995 0.000
#> wx5 ~~
#> wy5 0.043 0.011 3.939 0.000
#> wx6 ~~
#> wy6 0.023 0.011 2.175 0.030
#> wx7 ~~
#> wy7 0.032 0.011 2.881 0.004
#> wx8 ~~
#> wy8 0.029 0.011 2.593 0.010
#> wx9 ~~
#> wy9 0.012 0.013 0.971 0.331
#> wx10 ~~
#> wy10 0.043 0.013 3.403 0.001
#> wx11 ~~
#> wy11 0.063 0.013 4.896 0.000
#> .RIx ~~
#> .RIy 0.266 0.013 21.096 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.467 0.017 27.763 0.000
#> .RIy 0.442 0.016 28.012 0.000
#> wx1 0.462 0.019 24.034 0.000
#> wy1 0.389 0.017 23.503 0.000
#> wx2 0.402 0.017 23.994 0.000
#> wy2 0.424 0.017 24.485 0.000
#> wx3 0.346 0.015 23.757 0.000
#> wy3 0.313 0.013 23.292 0.000
#> wx4 0.323 0.014 22.711 0.000
#> wy4 0.322 0.014 22.565 0.000
#> wx5 0.326 0.014 23.605 0.000
#> wy5 0.332 0.014 23.560 0.000
#> wx6 0.348 0.015 23.638 0.000
#> wy6 0.304 0.013 23.253 0.000
#> wx7 0.349 0.015 23.491 0.000
#> wy7 0.328 0.014 23.564 0.000
#> wx8 0.322 0.014 22.979 0.000
#> wy8 0.327 0.014 23.170 0.000
#> wx9 0.370 0.016 23.022 0.000
#> wy9 0.373 0.016 22.741 0.000
#> wx10 0.369 0.017 22.106 0.000
#> wy10 0.338 0.016 21.599 0.000
#> wx11 0.365 0.017 21.431 0.000
#> wy11 0.328 0.016 20.622 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.001 0.013 -0.050 0.960
#> dif2 0.017 0.012 1.376 0.169
#> dif3 -0.010 0.002 -6.291 0.000
#>
#> lavaan 0.6-11 ended normally after 65 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5819.488
#> Degrees of freedom 277
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.321 0.002 150.244 0.000
#> RIy ~
#> oply (ey) 0.334 0.002 148.908 0.000
#> x2 ~
#> x1 (ax) -0.029 0.008 -3.764 0.000
#> y1 (bx) 0.062 0.008 7.961 0.000
#> x3 ~
#> x2 (ax) -0.029 0.008 -3.764 0.000
#> y2 (bx) 0.062 0.008 7.961 0.000
#> x4 ~
#> x3 (ax) -0.029 0.008 -3.764 0.000
#> y3 (bx) 0.062 0.008 7.961 0.000
#> x5 ~
#> x4 (ax) -0.029 0.008 -3.764 0.000
#> y4 (bx) 0.062 0.008 7.961 0.000
#> x6 ~
#> x5 (ax) -0.029 0.008 -3.764 0.000
#> y5 (bx) 0.062 0.008 7.961 0.000
#> x7 ~
#> x6 (ax) -0.029 0.008 -3.764 0.000
#> y6 (bx) 0.062 0.008 7.961 0.000
#> x8 ~
#> x7 (ax) -0.029 0.008 -3.764 0.000
#> y7 (bx) 0.062 0.008 7.961 0.000
#> x9 ~
#> x8 (ax) -0.029 0.008 -3.764 0.000
#> y8 (bx) 0.062 0.008 7.961 0.000
#> x10 ~
#> x9 (ax) -0.029 0.008 -3.764 0.000
#> y9 (bx) 0.062 0.008 7.961 0.000
#> x11 ~
#> x10 (ax) -0.029 0.008 -3.764 0.000
#> y10 (bx) 0.062 0.008 7.961 0.000
#> y2 ~
#> x1 (by) 0.058 0.008 7.698 0.000
#> y1 (ay) -0.023 0.008 -3.037 0.002
#> y3 ~
#> x2 (by) 0.058 0.008 7.698 0.000
#> y2 (ay) -0.023 0.008 -3.037 0.002
#> y4 ~
#> x3 (by) 0.058 0.008 7.698 0.000
#> y3 (ay) -0.023 0.008 -3.037 0.002
#> y5 ~
#> x4 (by) 0.058 0.008 7.698 0.000
#> y4 (ay) -0.023 0.008 -3.037 0.002
#> y6 ~
#> x5 (by) 0.058 0.008 7.698 0.000
#> y5 (ay) -0.023 0.008 -3.037 0.002
#> y7 ~
#> x6 (by) 0.058 0.008 7.698 0.000
#> y6 (ay) -0.023 0.008 -3.037 0.002
#> y8 ~
#> x7 (by) 0.058 0.008 7.698 0.000
#> y7 (ay) -0.023 0.008 -3.037 0.002
#> y9 ~
#> x8 (by) 0.058 0.008 7.698 0.000
#> y8 (ay) -0.023 0.008 -3.037 0.002
#> y10 ~
#> x9 (by) 0.058 0.008 7.698 0.000
#> y9 (ay) -0.023 0.008 -3.037 0.002
#> y11 ~
#> x10 (by) 0.058 0.008 7.698 0.000
#> y10 (ay) -0.023 0.008 -3.037 0.002
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.076 0.011 7.020 0.000
#> wx2 ~~
#> wy2 0.040 0.009 4.729 0.000
#> wx3 ~~
#> wy3 0.071 0.009 7.893 0.000
#> wx4 ~~
#> wy4 0.031 0.008 3.893 0.000
#> wx5 ~~
#> wy5 0.038 0.007 5.179 0.000
#> wx6 ~~
#> wy6 0.036 0.007 5.318 0.000
#> wx7 ~~
#> wy7 0.033 0.007 4.761 0.000
#> wx8 ~~
#> wy8 0.024 0.007 3.179 0.001
#> wx9 ~~
#> wy9 0.033 0.008 4.099 0.000
#> wx10 ~~
#> wy10 0.061 0.010 6.083 0.000
#> wx11 ~~
#> wy11 0.067 0.010 7.022 0.000
#> .RIx ~~
#> .RIy 0.998 0.037 26.915 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.565 0.043 36.053 0.000
#> .RIy 1.627 0.045 36.277 0.000
#> wx1 0.321 0.015 22.134 0.000
#> wy1 0.327 0.014 22.765 0.000
#> wx2 0.281 0.012 22.970 0.000
#> wy2 0.237 0.011 22.474 0.000
#> wx3 0.264 0.011 23.577 0.000
#> wy3 0.302 0.013 23.913 0.000
#> wx4 0.216 0.010 22.195 0.000
#> wy4 0.238 0.011 22.435 0.000
#> wx5 0.241 0.010 23.106 0.000
#> wy5 0.194 0.009 22.701 0.000
#> wx6 0.208 0.009 22.382 0.000
#> wy6 0.177 0.008 21.961 0.000
#> wx7 0.203 0.009 22.572 0.000
#> wy7 0.198 0.009 22.483 0.000
#> wx8 0.210 0.009 22.162 0.000
#> wy8 0.219 0.010 22.772 0.000
#> wx9 0.241 0.011 22.239 0.000
#> wy9 0.209 0.009 22.067 0.000
#> wx10 0.269 0.012 21.724 0.000
#> wy10 0.260 0.012 21.617 0.000
#> wx11 0.262 0.013 20.850 0.000
#> wy11 0.243 0.012 20.395 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.006 0.012 -0.528 0.597
#> dif2 0.004 0.012 0.300 0.764
#> dif3 -0.013 0.002 -6.125 0.000
#>
#> lavaan 0.6-11 ended normally after 45 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 78
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 6172.967
#> Degrees of freedom 277
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.263 0.002 119.615 0.000
#> RIy ~
#> oply (ey) 0.286 0.002 129.685 0.000
#> x2 ~
#> x1 (ax) 0.016 0.008 2.021 0.043
#> y1 (bx) 0.040 0.008 5.117 0.000
#> x3 ~
#> x2 (ax) 0.016 0.008 2.021 0.043
#> y2 (bx) 0.040 0.008 5.117 0.000
#> x4 ~
#> x3 (ax) 0.016 0.008 2.021 0.043
#> y3 (bx) 0.040 0.008 5.117 0.000
#> x5 ~
#> x4 (ax) 0.016 0.008 2.021 0.043
#> y4 (bx) 0.040 0.008 5.117 0.000
#> x6 ~
#> x5 (ax) 0.016 0.008 2.021 0.043
#> y5 (bx) 0.040 0.008 5.117 0.000
#> x7 ~
#> x6 (ax) 0.016 0.008 2.021 0.043
#> y6 (bx) 0.040 0.008 5.117 0.000
#> x8 ~
#> x7 (ax) 0.016 0.008 2.021 0.043
#> y7 (bx) 0.040 0.008 5.117 0.000
#> x9 ~
#> x8 (ax) 0.016 0.008 2.021 0.043
#> y8 (bx) 0.040 0.008 5.117 0.000
#> x10 ~
#> x9 (ax) 0.016 0.008 2.021 0.043
#> y9 (bx) 0.040 0.008 5.117 0.000
#> x11 ~
#> x10 (ax) 0.016 0.008 2.021 0.043
#> y10 (bx) 0.040 0.008 5.117 0.000
#> y2 ~
#> x1 (by) 0.049 0.008 6.169 0.000
#> y1 (ay) -0.003 0.008 -0.404 0.686
#> y3 ~
#> x2 (by) 0.049 0.008 6.169 0.000
#> y2 (ay) -0.003 0.008 -0.404 0.686
#> y4 ~
#> x3 (by) 0.049 0.008 6.169 0.000
#> y3 (ay) -0.003 0.008 -0.404 0.686
#> y5 ~
#> x4 (by) 0.049 0.008 6.169 0.000
#> y4 (ay) -0.003 0.008 -0.404 0.686
#> y6 ~
#> x5 (by) 0.049 0.008 6.169 0.000
#> y5 (ay) -0.003 0.008 -0.404 0.686
#> y7 ~
#> x6 (by) 0.049 0.008 6.169 0.000
#> y6 (ay) -0.003 0.008 -0.404 0.686
#> y8 ~
#> x7 (by) 0.049 0.008 6.169 0.000
#> y7 (ay) -0.003 0.008 -0.404 0.686
#> y9 ~
#> x8 (by) 0.049 0.008 6.169 0.000
#> y8 (ay) -0.003 0.008 -0.404 0.686
#> y10 ~
#> x9 (by) 0.049 0.008 6.169 0.000
#> y9 (ay) -0.003 0.008 -0.404 0.686
#> y11 ~
#> x10 (by) 0.049 0.008 6.169 0.000
#> y10 (ay) -0.003 0.008 -0.404 0.686
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.133 0.017 7.847 0.000
#> wx2 ~~
#> wy2 0.041 0.013 3.141 0.002
#> wx3 ~~
#> wy3 0.064 0.013 5.012 0.000
#> wx4 ~~
#> wy4 0.035 0.012 2.818 0.005
#> wx5 ~~
#> wy5 0.018 0.012 1.514 0.130
#> wx6 ~~
#> wy6 0.058 0.012 4.811 0.000
#> wx7 ~~
#> wy7 0.052 0.012 4.514 0.000
#> wx8 ~~
#> wy8 0.044 0.013 3.515 0.000
#> wx9 ~~
#> wy9 0.035 0.013 2.638 0.008
#> wx10 ~~
#> wy10 0.048 0.014 3.412 0.001
#> wx11 ~~
#> wy11 0.053 0.016 3.301 0.001
#> .RIx ~~
#> .RIy 0.910 0.034 26.466 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.475 0.043 34.155 0.000
#> .RIy 1.355 0.040 34.092 0.000
#> wx1 0.515 0.023 22.469 0.000
#> wy1 0.499 0.022 22.710 0.000
#> wx2 0.398 0.017 22.953 0.000
#> wy2 0.394 0.017 22.918 0.000
#> wx3 0.392 0.017 23.514 0.000
#> wy3 0.408 0.017 23.379 0.000
#> wx4 0.369 0.017 22.294 0.000
#> wy4 0.320 0.015 21.716 0.000
#> wx5 0.342 0.015 22.862 0.000
#> wy5 0.349 0.015 22.930 0.000
#> wx6 0.366 0.016 23.094 0.000
#> wy6 0.351 0.015 22.843 0.000
#> wx7 0.364 0.016 22.956 0.000
#> wy7 0.305 0.014 22.303 0.000
#> wx8 0.349 0.015 22.667 0.000
#> wy8 0.383 0.017 22.891 0.000
#> wx9 0.380 0.017 22.382 0.000
#> wy9 0.383 0.017 22.293 0.000
#> wx10 0.371 0.017 21.401 0.000
#> wy10 0.388 0.018 21.242 0.000
#> wx11 0.462 0.021 21.518 0.000
#> wy11 0.383 0.019 20.177 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.019 0.012 1.649 0.099
#> dif2 -0.009 0.012 -0.781 0.435
#> dif3 -0.024 0.002 -10.618 0.0003.6.7.3 SC-RI-CLPM
SCCLPM <- '
# Create between components (random intercepts)
RIx =~ 1*x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11
RIy =~ 1*y1 + y2 + y3 + y4 + y5 + y6 + y7 + y8 + y9 + y10 + y11
RIx ~ ex*oplx
RIy ~ ey*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
x2 ~ ax*x1 + bx*y1
x3 ~ ax*x2 + bx*y2
x4 ~ ax*x3 + bx*y3
x5 ~ ax*x4 + bx*y4
x6 ~ ax*x5 + bx*y5
x7 ~ ax*x6 + bx*y6
x8 ~ ax*x7 + bx*y7
x9 ~ ax*x8 + bx*y8
x10 ~ ax*x9 + bx*y9
x11 ~ ax*x10 + bx*y10
y2 ~ by*x1 + ay*y1
y3 ~ by*x2 + ay*y2
y4 ~ by*x3 + ay*y3
y5 ~ by*x4 + ay*y4
y6 ~ by*x5 + ay*y5
y7 ~ by*x6 + ay*y6
y8 ~ by*x7 + ay*y7
y9 ~ by*x8 + ay*y8
y10 ~ by*x9 + ay*y9
y11 ~ by*x10 + ay*y10
dif1 := ax - ay
dif2 := bx - by
dif3 := ex - ey
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(SCCLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
summary(results_temp[[4]])
results[[25]] <- results_temp[[1]]
results[[26]] <- results_temp[[2]]
results[[27]] <- results_temp[[3]]
results[[28]] <- results_temp[[4]]
names(results)[25:28] <- c("fitm3h2y1", "fitm3h2y2","fitm3h2y3","fitm3h2y4")
save(results, file="results.RData")load("addfiles/results.Rdata")
summary(results[[25]])
summary(results[[26]])
summary(results[[27]])
summary(results[[28]])#> lavaan 0.6-11 ended normally after 51 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1144.862
#> Degrees of freedom 257
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.763 0.021 36.188 0.000
#> x3 0.767 0.021 37.058 0.000
#> x4 0.637 0.021 30.424 0.000
#> x5 0.782 0.021 37.498 0.000
#> x6 0.666 0.020 33.092 0.000
#> x7 0.626 0.019 33.115 0.000
#> x8 0.685 0.019 35.811 0.000
#> x9 0.626 0.020 32.096 0.000
#> x10 0.709 0.020 35.892 0.000
#> x11 0.741 0.021 35.665 0.000
#> RIy =~
#> y1 1.000
#> y2 0.775 0.022 35.802 0.000
#> y3 0.776 0.021 36.197 0.000
#> y4 0.625 0.022 28.846 0.000
#> y5 0.672 0.021 32.760 0.000
#> y6 0.652 0.020 32.553 0.000
#> y7 0.617 0.019 31.933 0.000
#> y8 0.661 0.019 34.008 0.000
#> y9 0.657 0.020 32.846 0.000
#> y10 0.735 0.020 36.116 0.000
#> y11 0.762 0.022 35.406 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.126 0.002 61.856 0.000
#> RIy ~
#> oply (ey) 0.128 0.002 65.198 0.000
#> x2 ~
#> x1 (ax) 0.218 0.012 18.700 0.000
#> y1 (bx) 0.064 0.011 5.987 0.000
#> x3 ~
#> x2 (ax) 0.218 0.012 18.700 0.000
#> y2 (bx) 0.064 0.011 5.987 0.000
#> x4 ~
#> x3 (ax) 0.218 0.012 18.700 0.000
#> y3 (bx) 0.064 0.011 5.987 0.000
#> x5 ~
#> x4 (ax) 0.218 0.012 18.700 0.000
#> y4 (bx) 0.064 0.011 5.987 0.000
#> x6 ~
#> x5 (ax) 0.218 0.012 18.700 0.000
#> y5 (bx) 0.064 0.011 5.987 0.000
#> x7 ~
#> x6 (ax) 0.218 0.012 18.700 0.000
#> y6 (bx) 0.064 0.011 5.987 0.000
#> x8 ~
#> x7 (ax) 0.218 0.012 18.700 0.000
#> y7 (bx) 0.064 0.011 5.987 0.000
#> x9 ~
#> x8 (ax) 0.218 0.012 18.700 0.000
#> y8 (bx) 0.064 0.011 5.987 0.000
#> x10 ~
#> x9 (ax) 0.218 0.012 18.700 0.000
#> y9 (bx) 0.064 0.011 5.987 0.000
#> x11 ~
#> x10 (ax) 0.218 0.012 18.700 0.000
#> y10 (bx) 0.064 0.011 5.987 0.000
#> y2 ~
#> x1 (by) 0.078 0.009 8.823 0.000
#> y1 (ay) 0.190 0.012 15.440 0.000
#> y3 ~
#> x2 (by) 0.078 0.009 8.823 0.000
#> y2 (ay) 0.190 0.012 15.440 0.000
#> y4 ~
#> x3 (by) 0.078 0.009 8.823 0.000
#> y3 (ay) 0.190 0.012 15.440 0.000
#> y5 ~
#> x4 (by) 0.078 0.009 8.823 0.000
#> y4 (ay) 0.190 0.012 15.440 0.000
#> y6 ~
#> x5 (by) 0.078 0.009 8.823 0.000
#> y5 (ay) 0.190 0.012 15.440 0.000
#> y7 ~
#> x6 (by) 0.078 0.009 8.823 0.000
#> y6 (ay) 0.190 0.012 15.440 0.000
#> y8 ~
#> x7 (by) 0.078 0.009 8.823 0.000
#> y7 (ay) 0.190 0.012 15.440 0.000
#> y9 ~
#> x8 (by) 0.078 0.009 8.823 0.000
#> y8 (ay) 0.190 0.012 15.440 0.000
#> y10 ~
#> x9 (by) 0.078 0.009 8.823 0.000
#> y9 (ay) 0.190 0.012 15.440 0.000
#> y11 ~
#> x10 (by) 0.078 0.009 8.823 0.000
#> y10 (ay) 0.190 0.012 15.440 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.124 0.022 5.562 0.000
#> wx2 ~~
#> wy2 0.088 0.020 4.470 0.000
#> wx3 ~~
#> wy3 0.088 0.018 4.835 0.000
#> wx4 ~~
#> wy4 0.099 0.018 5.406 0.000
#> wx5 ~~
#> wy5 0.103 0.021 4.818 0.000
#> wx6 ~~
#> wy6 0.069 0.017 4.166 0.000
#> wx7 ~~
#> wy7 0.086 0.015 5.582 0.000
#> wx8 ~~
#> wy8 0.080 0.018 4.432 0.000
#> wx9 ~~
#> wy9 0.096 0.019 5.013 0.000
#> wx10 ~~
#> wy10 0.038 0.020 1.888 0.059
#> wx11 ~~
#> wy11 0.086 0.021 4.206 0.000
#> .RIx ~~
#> .RIy 0.327 0.020 16.012 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.834 0.034 24.576 0.000
#> .RIy 0.547 0.024 22.904 0.000
#> wx1 0.689 0.032 21.686 0.000
#> wy1 0.587 0.028 21.267 0.000
#> wx2 0.684 0.029 23.634 0.000
#> wy2 0.553 0.024 22.641 0.000
#> wx3 0.577 0.025 23.050 0.000
#> wy3 0.491 0.022 22.141 0.000
#> wx4 0.613 0.027 23.124 0.000
#> wy4 0.491 0.022 22.394 0.000
#> wx5 0.714 0.031 23.172 0.000
#> wy5 0.572 0.024 23.422 0.000
#> wx6 0.525 0.023 23.217 0.000
#> wy6 0.439 0.020 22.490 0.000
#> wx7 0.493 0.021 23.425 0.000
#> wy7 0.442 0.019 23.077 0.000
#> wx8 0.555 0.024 23.101 0.000
#> wy8 0.507 0.022 22.998 0.000
#> wx9 0.610 0.026 23.509 0.000
#> wy9 0.516 0.023 22.383 0.000
#> wx10 0.567 0.026 21.556 0.000
#> wy10 0.500 0.024 20.918 0.000
#> wx11 0.599 0.028 21.091 0.000
#> wy11 0.496 0.025 20.045 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.028 0.017 1.649 0.099
#> dif2 -0.014 0.013 -1.063 0.288
#> dif3 -0.002 0.002 -0.695 0.487
#>
#> lavaan 0.6-11 ended normally after 50 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 689.156
#> Degrees of freedom 257
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.883 0.021 41.305 0.000
#> x3 0.889 0.021 41.388 0.000
#> x4 0.890 0.022 40.779 0.000
#> x5 0.900 0.022 41.363 0.000
#> x6 0.883 0.022 39.901 0.000
#> x7 0.902 0.022 40.899 0.000
#> x8 0.858 0.022 39.387 0.000
#> x9 0.839 0.022 38.446 0.000
#> x10 0.906 0.022 40.350 0.000
#> x11 0.873 0.023 38.683 0.000
#> RIy =~
#> y1 1.000
#> y2 0.875 0.021 42.424 0.000
#> y3 0.902 0.020 44.815 0.000
#> y4 0.897 0.021 42.970 0.000
#> y5 0.902 0.021 43.112 0.000
#> y6 0.894 0.021 43.056 0.000
#> y7 0.895 0.021 43.037 0.000
#> y8 0.858 0.021 41.292 0.000
#> y9 0.852 0.021 40.471 0.000
#> y10 0.886 0.021 42.419 0.000
#> y11 0.889 0.021 41.479 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.096 0.002 61.519 0.000
#> RIy ~
#> oply (ey) 0.106 0.002 68.404 0.000
#> x2 ~
#> x1 (ax) 0.100 0.011 8.975 0.000
#> y1 (bx) 0.053 0.010 5.351 0.000
#> x3 ~
#> x2 (ax) 0.100 0.011 8.975 0.000
#> y2 (bx) 0.053 0.010 5.351 0.000
#> x4 ~
#> x3 (ax) 0.100 0.011 8.975 0.000
#> y3 (bx) 0.053 0.010 5.351 0.000
#> x5 ~
#> x4 (ax) 0.100 0.011 8.975 0.000
#> y4 (bx) 0.053 0.010 5.351 0.000
#> x6 ~
#> x5 (ax) 0.100 0.011 8.975 0.000
#> y5 (bx) 0.053 0.010 5.351 0.000
#> x7 ~
#> x6 (ax) 0.100 0.011 8.975 0.000
#> y6 (bx) 0.053 0.010 5.351 0.000
#> x8 ~
#> x7 (ax) 0.100 0.011 8.975 0.000
#> y7 (bx) 0.053 0.010 5.351 0.000
#> x9 ~
#> x8 (ax) 0.100 0.011 8.975 0.000
#> y8 (bx) 0.053 0.010 5.351 0.000
#> x10 ~
#> x9 (ax) 0.100 0.011 8.975 0.000
#> y9 (bx) 0.053 0.010 5.351 0.000
#> x11 ~
#> x10 (ax) 0.100 0.011 8.975 0.000
#> y10 (bx) 0.053 0.010 5.351 0.000
#> y2 ~
#> x1 (by) 0.036 0.009 3.775 0.000
#> y1 (ay) 0.104 0.011 9.128 0.000
#> y3 ~
#> x2 (by) 0.036 0.009 3.775 0.000
#> y2 (ay) 0.104 0.011 9.128 0.000
#> y4 ~
#> x3 (by) 0.036 0.009 3.775 0.000
#> y3 (ay) 0.104 0.011 9.128 0.000
#> y5 ~
#> x4 (by) 0.036 0.009 3.775 0.000
#> y4 (ay) 0.104 0.011 9.128 0.000
#> y6 ~
#> x5 (by) 0.036 0.009 3.775 0.000
#> y5 (ay) 0.104 0.011 9.128 0.000
#> y7 ~
#> x6 (by) 0.036 0.009 3.775 0.000
#> y6 (ay) 0.104 0.011 9.128 0.000
#> y8 ~
#> x7 (by) 0.036 0.009 3.775 0.000
#> y7 (ay) 0.104 0.011 9.128 0.000
#> y9 ~
#> x8 (by) 0.036 0.009 3.775 0.000
#> y8 (ay) 0.104 0.011 9.128 0.000
#> y10 ~
#> x9 (by) 0.036 0.009 3.775 0.000
#> y9 (ay) 0.104 0.011 9.128 0.000
#> y11 ~
#> x10 (by) 0.036 0.009 3.775 0.000
#> y10 (ay) 0.104 0.011 9.128 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.059 0.013 4.582 0.000
#> wx2 ~~
#> wy2 0.048 0.013 3.756 0.000
#> wx3 ~~
#> wy3 0.031 0.011 2.813 0.005
#> wx4 ~~
#> wy4 0.044 0.011 4.011 0.000
#> wx5 ~~
#> wy5 0.044 0.011 4.004 0.000
#> wx6 ~~
#> wy6 0.027 0.011 2.507 0.012
#> wx7 ~~
#> wy7 0.033 0.011 2.939 0.003
#> wx8 ~~
#> wy8 0.032 0.011 2.895 0.004
#> wx9 ~~
#> wy9 0.011 0.013 0.864 0.388
#> wx10 ~~
#> wy10 0.047 0.013 3.656 0.000
#> wx11 ~~
#> wy11 0.062 0.013 4.858 0.000
#> .RIx ~~
#> .RIy 0.276 0.014 20.076 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.517 0.020 25.624 0.000
#> .RIy 0.482 0.018 26.510 0.000
#> wx1 0.449 0.019 23.603 0.000
#> wy1 0.377 0.016 23.042 0.000
#> wx2 0.407 0.017 23.965 0.000
#> wy2 0.429 0.017 24.601 0.000
#> wx3 0.354 0.015 23.575 0.000
#> wy3 0.317 0.014 23.087 0.000
#> wx4 0.325 0.014 22.599 0.000
#> wy4 0.327 0.015 22.411 0.000
#> wx5 0.327 0.014 23.315 0.000
#> wy5 0.335 0.014 23.309 0.000
#> wx6 0.355 0.015 23.545 0.000
#> wy6 0.308 0.013 23.106 0.000
#> wx7 0.349 0.015 23.275 0.000
#> wy7 0.331 0.014 23.418 0.000
#> wx8 0.329 0.014 23.031 0.000
#> wy8 0.334 0.014 23.240 0.000
#> wx9 0.373 0.016 23.223 0.000
#> wy9 0.378 0.017 22.877 0.000
#> wx10 0.370 0.017 21.705 0.000
#> wy10 0.344 0.016 21.448 0.000
#> wx11 0.366 0.017 21.458 0.000
#> wy11 0.326 0.016 20.542 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.004 0.016 -0.256 0.798
#> dif2 0.017 0.013 1.310 0.190
#> dif3 -0.010 0.002 -5.415 0.000
#>
#> lavaan 0.6-11 ended normally after 103 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5022.772
#> Degrees of freedom 257
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.686 0.015 45.498 0.000
#> x3 0.683 0.015 45.363 0.000
#> x4 0.692 0.015 45.982 0.000
#> x5 0.691 0.015 45.416 0.000
#> x6 0.695 0.015 45.675 0.000
#> x7 0.700 0.015 45.845 0.000
#> x8 0.701 0.015 45.549 0.000
#> x9 0.692 0.015 44.722 0.000
#> x10 0.691 0.015 44.768 0.000
#> x11 0.702 0.015 45.625 0.000
#> RIy =~
#> y1 1.000
#> y2 0.718 0.014 49.717 0.000
#> y3 0.712 0.015 48.836 0.000
#> y4 0.724 0.015 49.767 0.000
#> y5 0.726 0.015 49.612 0.000
#> y6 0.726 0.015 49.526 0.000
#> y7 0.729 0.015 49.555 0.000
#> y8 0.729 0.015 49.069 0.000
#> y9 0.722 0.015 48.614 0.000
#> y10 0.720 0.015 48.332 0.000
#> y11 0.730 0.015 49.132 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.328 0.002 150.866 0.000
#> RIy ~
#> oply (ey) 0.341 0.002 149.368 0.000
#> x2 ~
#> x1 (ax) 0.149 0.012 12.205 0.000
#> y1 (bx) 0.170 0.009 19.343 0.000
#> x3 ~
#> x2 (ax) 0.149 0.012 12.205 0.000
#> y2 (bx) 0.170 0.009 19.343 0.000
#> x4 ~
#> x3 (ax) 0.149 0.012 12.205 0.000
#> y3 (bx) 0.170 0.009 19.343 0.000
#> x5 ~
#> x4 (ax) 0.149 0.012 12.205 0.000
#> y4 (bx) 0.170 0.009 19.343 0.000
#> x6 ~
#> x5 (ax) 0.149 0.012 12.205 0.000
#> y5 (bx) 0.170 0.009 19.343 0.000
#> x7 ~
#> x6 (ax) 0.149 0.012 12.205 0.000
#> y6 (bx) 0.170 0.009 19.343 0.000
#> x8 ~
#> x7 (ax) 0.149 0.012 12.205 0.000
#> y7 (bx) 0.170 0.009 19.343 0.000
#> x9 ~
#> x8 (ax) 0.149 0.012 12.205 0.000
#> y8 (bx) 0.170 0.009 19.343 0.000
#> x10 ~
#> x9 (ax) 0.149 0.012 12.205 0.000
#> y9 (bx) 0.170 0.009 19.343 0.000
#> x11 ~
#> x10 (ax) 0.149 0.012 12.205 0.000
#> y10 (bx) 0.170 0.009 19.343 0.000
#> y2 ~
#> x1 (by) 0.156 0.009 17.816 0.000
#> y1 (ay) 0.137 0.012 11.742 0.000
#> y3 ~
#> x2 (by) 0.156 0.009 17.816 0.000
#> y2 (ay) 0.137 0.012 11.742 0.000
#> y4 ~
#> x3 (by) 0.156 0.009 17.816 0.000
#> y3 (ay) 0.137 0.012 11.742 0.000
#> y5 ~
#> x4 (by) 0.156 0.009 17.816 0.000
#> y4 (ay) 0.137 0.012 11.742 0.000
#> y6 ~
#> x5 (by) 0.156 0.009 17.816 0.000
#> y5 (ay) 0.137 0.012 11.742 0.000
#> y7 ~
#> x6 (by) 0.156 0.009 17.816 0.000
#> y6 (ay) 0.137 0.012 11.742 0.000
#> y8 ~
#> x7 (by) 0.156 0.009 17.816 0.000
#> y7 (ay) 0.137 0.012 11.742 0.000
#> y9 ~
#> x8 (by) 0.156 0.009 17.816 0.000
#> y8 (ay) 0.137 0.012 11.742 0.000
#> y10 ~
#> x9 (by) 0.156 0.009 17.816 0.000
#> y9 (ay) 0.137 0.012 11.742 0.000
#> y11 ~
#> x10 (by) 0.156 0.009 17.816 0.000
#> y10 (ay) 0.137 0.012 11.742 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.065 0.012 5.508 0.000
#> wx2 ~~
#> wy2 0.052 0.009 5.578 0.000
#> wx3 ~~
#> wy3 0.071 0.009 7.727 0.000
#> wx4 ~~
#> wy4 0.041 0.008 5.019 0.000
#> wx5 ~~
#> wy5 0.050 0.008 6.279 0.000
#> wx6 ~~
#> wy6 0.047 0.007 6.644 0.000
#> wx7 ~~
#> wy7 0.042 0.007 5.804 0.000
#> wx8 ~~
#> wy8 0.037 0.008 4.603 0.000
#> wx9 ~~
#> wy9 0.041 0.008 5.043 0.000
#> wx10 ~~
#> wy10 0.072 0.010 6.895 0.000
#> wx11 ~~
#> wy11 0.067 0.009 7.105 0.000
#> .RIx ~~
#> .RIy 0.934 0.038 24.664 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.626 0.046 35.382 0.000
#> .RIy 1.690 0.047 35.742 0.000
#> wx1 0.325 0.016 20.142 0.000
#> wy1 0.337 0.016 21.188 0.000
#> wx2 0.307 0.013 22.959 0.000
#> wy2 0.256 0.011 22.443 0.000
#> wx3 0.268 0.011 23.451 0.000
#> wy3 0.308 0.013 23.721 0.000
#> wx4 0.224 0.010 22.193 0.000
#> wy4 0.254 0.011 22.403 0.000
#> wx5 0.256 0.011 22.825 0.000
#> wy5 0.213 0.009 22.451 0.000
#> wx6 0.227 0.010 22.418 0.000
#> wy6 0.185 0.008 21.951 0.000
#> wx7 0.215 0.010 22.461 0.000
#> wy7 0.209 0.009 22.363 0.000
#> wx8 0.225 0.010 21.896 0.000
#> wy8 0.234 0.010 22.539 0.000
#> wx9 0.256 0.011 22.348 0.000
#> wy9 0.215 0.010 22.082 0.000
#> wx10 0.289 0.013 21.592 0.000
#> wy10 0.269 0.013 21.477 0.000
#> wx11 0.256 0.012 20.810 0.000
#> wy11 0.245 0.012 20.453 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.012 0.017 0.718 0.473
#> dif2 0.014 0.013 1.094 0.274
#> dif3 -0.013 0.002 -5.771 0.000
#>
#> lavaan 0.6-11 ended normally after 69 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 98
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 5574.731
#> Degrees of freedom 257
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 0.706 0.016 43.047 0.000
#> x3 0.703 0.017 42.527 0.000
#> x4 0.705 0.017 42.711 0.000
#> x5 0.733 0.016 44.506 0.000
#> x6 0.697 0.017 41.287 0.000
#> x7 0.710 0.016 43.026 0.000
#> x8 0.721 0.017 43.497 0.000
#> x9 0.726 0.017 43.078 0.000
#> x10 0.725 0.017 42.690 0.000
#> x11 0.738 0.017 43.165 0.000
#> RIy =~
#> y1 1.000
#> y2 0.781 0.016 49.839 0.000
#> y3 0.765 0.016 48.052 0.000
#> y4 0.776 0.016 48.942 0.000
#> y5 0.788 0.016 49.499 0.000
#> y6 0.761 0.016 46.910 0.000
#> y7 0.763 0.016 48.250 0.000
#> y8 0.773 0.016 48.345 0.000
#> y9 0.769 0.016 47.589 0.000
#> y10 0.762 0.016 46.777 0.000
#> y11 0.765 0.016 47.086 0.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.271 0.002 119.594 0.000
#> RIy ~
#> oply (ey) 0.296 0.002 130.188 0.000
#> x2 ~
#> x1 (ax) 0.161 0.012 13.435 0.000
#> y1 (bx) 0.142 0.009 15.367 0.000
#> x3 ~
#> x2 (ax) 0.161 0.012 13.435 0.000
#> y2 (bx) 0.142 0.009 15.367 0.000
#> x4 ~
#> x3 (ax) 0.161 0.012 13.435 0.000
#> y3 (bx) 0.142 0.009 15.367 0.000
#> x5 ~
#> x4 (ax) 0.161 0.012 13.435 0.000
#> y4 (bx) 0.142 0.009 15.367 0.000
#> x6 ~
#> x5 (ax) 0.161 0.012 13.435 0.000
#> y5 (bx) 0.142 0.009 15.367 0.000
#> x7 ~
#> x6 (ax) 0.161 0.012 13.435 0.000
#> y6 (bx) 0.142 0.009 15.367 0.000
#> x8 ~
#> x7 (ax) 0.161 0.012 13.435 0.000
#> y7 (bx) 0.142 0.009 15.367 0.000
#> x9 ~
#> x8 (ax) 0.161 0.012 13.435 0.000
#> y8 (bx) 0.142 0.009 15.367 0.000
#> x10 ~
#> x9 (ax) 0.161 0.012 13.435 0.000
#> y9 (bx) 0.142 0.009 15.367 0.000
#> x11 ~
#> x10 (ax) 0.161 0.012 13.435 0.000
#> y10 (bx) 0.142 0.009 15.367 0.000
#> y2 ~
#> x1 (by) 0.127 0.009 13.616 0.000
#> y1 (ay) 0.120 0.012 10.183 0.000
#> y3 ~
#> x2 (by) 0.127 0.009 13.616 0.000
#> y2 (ay) 0.120 0.012 10.183 0.000
#> y4 ~
#> x3 (by) 0.127 0.009 13.616 0.000
#> y3 (ay) 0.120 0.012 10.183 0.000
#> y5 ~
#> x4 (by) 0.127 0.009 13.616 0.000
#> y4 (ay) 0.120 0.012 10.183 0.000
#> y6 ~
#> x5 (by) 0.127 0.009 13.616 0.000
#> y5 (ay) 0.120 0.012 10.183 0.000
#> y7 ~
#> x6 (by) 0.127 0.009 13.616 0.000
#> y6 (ay) 0.120 0.012 10.183 0.000
#> y8 ~
#> x7 (by) 0.127 0.009 13.616 0.000
#> y7 (ay) 0.120 0.012 10.183 0.000
#> y9 ~
#> x8 (by) 0.127 0.009 13.616 0.000
#> y8 (ay) 0.120 0.012 10.183 0.000
#> y10 ~
#> x9 (by) 0.127 0.009 13.616 0.000
#> y9 (ay) 0.120 0.012 10.183 0.000
#> y11 ~
#> x10 (by) 0.127 0.009 13.616 0.000
#> y10 (ay) 0.120 0.012 10.183 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.131 0.018 7.457 0.000
#> wx2 ~~
#> wy2 0.070 0.014 5.062 0.000
#> wx3 ~~
#> wy3 0.070 0.013 5.276 0.000
#> wx4 ~~
#> wy4 0.060 0.013 4.499 0.000
#> wx5 ~~
#> wy5 0.017 0.012 1.424 0.154
#> wx6 ~~
#> wy6 0.087 0.013 6.756 0.000
#> wx7 ~~
#> wy7 0.059 0.012 5.030 0.000
#> wx8 ~~
#> wy8 0.057 0.013 4.372 0.000
#> wx9 ~~
#> wy9 0.050 0.014 3.650 0.000
#> wx10 ~~
#> wy10 0.067 0.015 4.543 0.000
#> wx11 ~~
#> wy11 0.046 0.016 2.927 0.003
#> .RIx ~~
#> .RIy 0.869 0.036 24.206 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.589 0.048 33.316 0.000
#> .RIy 1.404 0.042 33.553 0.000
#> wx1 0.504 0.024 21.037 0.000
#> wy1 0.497 0.023 21.768 0.000
#> wx2 0.434 0.019 23.110 0.000
#> wy2 0.410 0.018 22.933 0.000
#> wx3 0.405 0.017 23.521 0.000
#> wy3 0.423 0.018 23.368 0.000
#> wx4 0.397 0.018 22.445 0.000
#> wy4 0.348 0.016 21.687 0.000
#> wx5 0.341 0.015 22.330 0.000
#> wy5 0.353 0.016 22.553 0.000
#> wx6 0.397 0.017 23.271 0.000
#> wy6 0.383 0.017 22.925 0.000
#> wx7 0.374 0.016 23.056 0.000
#> wy7 0.317 0.014 22.339 0.000
#> wx8 0.374 0.017 22.579 0.000
#> wy8 0.396 0.017 22.750 0.000
#> wx9 0.397 0.018 22.364 0.000
#> wy9 0.398 0.018 22.288 0.000
#> wx10 0.392 0.019 21.191 0.000
#> wy10 0.404 0.019 21.155 0.000
#> wx11 0.439 0.021 21.345 0.000
#> wy11 0.384 0.019 20.288 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.041 0.017 2.442 0.015
#> dif2 0.015 0.014 1.103 0.270
#> dif3 -0.025 0.002 -10.223 0.0003.6.7.4 LT-RI-CLPM
LTRICLPM <- '
# Create between components (random intercepts)
RIx =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11
RIy =~ 1*y1 + 1*y2 + 1*y3 + 1*y4 + 1*y5 + 1*y6 + 1*y7 + 1*y8 + 1*y9 + 1*y10 + 1*y11
RIx ~ ex*oplx
RIy ~ ey*oply
#Random slopes
RIsx =~ 1*x1 + 2*x2 + 3*x3 + 4*x4 + 5*x5 + 6*x6 + 7*x7 + 8*x8 + 9*x9 + 10*x10 + 11*x11
RIsy =~ 1*y1 + 2*y2 + 3*y3 + 4*y4 + 5*y5 + 6*y6 + 7*y7 + 8*y8 + 9*y9 + 10*y10 + 11*y11
RIsx ~ fx*oplx
RIsy ~ fy*oply
# Create within-person centered variables
wx1 =~ 1*x1
wx2 =~ 1*x2
wx3 =~ 1*x3
wx4 =~ 1*x4
wx5 =~ 1*x5
wx6 =~ 1*x6
wx7 =~ 1*x7
wx8 =~ 1*x8
wx9 =~ 1*x9
wx10 =~ 1*x10
wx11 =~ 1*x11
wy1 =~ 1*y1
wy2 =~ 1*y2
wy3 =~ 1*y3
wy4 =~ 1*y4
wy5 =~ 1*y5
wy6 =~ 1*y6
wy7 =~ 1*y7
wy8 =~ 1*y8
wy9 =~ 1*y9
wy10 =~ 1*y10
wy11 =~ 1*y11
# Estimate the lagged effects between the within-person centered variables.
x2 ~ ax*x1 + bx*y1
x3 ~ ax*x2 + bx*y2
x4 ~ ax*x3 + bx*y3
x5 ~ ax*x4 + bx*y4
x6 ~ ax*x5 + bx*y5
x7 ~ ax*x6 + bx*y6
x8 ~ ax*x7 + bx*y7
x9 ~ ax*x8 + bx*y8
x10 ~ ax*x9 + bx*y9
x11 ~ ax*x10 + bx*y10
y2 ~ by*x1 + ay*y1
y3 ~ by*x2 + ay*y2
y4 ~ by*x3 + ay*y3
y5 ~ by*x4 + ay*y4
y6 ~ by*x5 + ay*y5
y7 ~ by*x6 + ay*y6
y8 ~ by*x7 + ay*y7
y9 ~ by*x8 + ay*y8
y10 ~ by*x9 + ay*y9
y11 ~ by*x10 + ay*y10
dif1 := ax - ay
dif2 := bx - by
dif3 := ex - ey
dif4 := fx - fy
# Estimate the (residual) covariance between the within-person centered variables
wx1 ~~ wy1 # Covariance
wx2 ~~ wy2
wx3 ~~ wy3
wx4 ~~ wy4
wx5 ~~ wy5
wx6 ~~ wy6
wx7 ~~ wy7
wx8 ~~ wy8
wx9 ~~ wy9
wx10 ~~ wy10
wx11 ~~ wy11
# Estimate the variance and covariance of the random intercepts and random slopes.
RIx ~~ RIx
RIy ~~ RIy
RIx ~~ RIy #covariance intercepts: interpretation SELECTION
RIsx ~~ RIsx
RIsy ~~ RIsy
RIsx ~~ RIsy #covariance slopes: interpretation COMMON CONTEXT
RIx ~~ RIsx #covariance intercept/slope: interpretation regression to the mean
RIy ~~ RIsy
RIx ~~ RIsy #cross-covariance: interpretation INFLUENCE?
RIy ~~ RIsx
# Estimate the (residual) variance of the within-person centered variables.
wx1 ~~ wx1 # Variances
wy1 ~~ wy1
wx2 ~~ wx2 # Residual variances
wy2 ~~ wy2
wx3 ~~ wx3
wy3 ~~ wy3
wx4 ~~ wx4
wy4 ~~ wy4
wx5 ~~ wx5
wy5 ~~ wy5
wx6 ~~ wx6
wy6 ~~ wy6
wx7 ~~ wx7
wy7 ~~ wy7
wx8 ~~ wx8
wy8 ~~ wy8
wx9 ~~ wx9
wy9 ~~ wy9
wx10 ~~ wx10
wy10 ~~ wy10
wx11 ~~ wx11
wy11 ~~ wy11
'
#Estimate models a bit faster:
estimate <- function(x) lavaan(LTRICLPM, data=x, missing = "fiml.x", meanstructure = T )
library(future.apply)
plan(multisession)
results_temp <- future_lapply(datalist_ori, estimate)
summary(results_temp[[4]])
results[[29]] <- results_temp[[1]]
results[[30]] <- results_temp[[2]]
results[[31]] <- results_temp[[3]]
results[[32]] <- results_temp[[4]]
names(results)[29:32] <- c("fitm4h2y1", "fitm4h2y2","fitm4h2y3","fitm4h2y4")
save(results, file="results.RData")load("addfiles/results.Rdata")
summary(results[[29]])
summary(results[[30]])
summary(results[[31]])
summary(results[[32]])#> lavaan 0.6-11 ended normally after 105 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1415
#>
#> Model Test User Model:
#>
#> Test statistic 1478.192
#> Degrees of freedom 268
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.126 0.002 63.991 0.000
#> RIy ~
#> oply (ey) 0.123 0.002 65.556 0.000
#> RIsx ~
#> oplx (fx) -0.003 0.000 -11.534 0.000
#> RIsy ~
#> oply (fy) -0.002 0.000 -9.901 0.000
#> x2 ~
#> x1 (ax) 0.076 0.011 7.263 0.000
#> y1 (bx) 0.024 0.011 2.168 0.030
#> x3 ~
#> x2 (ax) 0.076 0.011 7.263 0.000
#> y2 (bx) 0.024 0.011 2.168 0.030
#> x4 ~
#> x3 (ax) 0.076 0.011 7.263 0.000
#> y3 (bx) 0.024 0.011 2.168 0.030
#> x5 ~
#> x4 (ax) 0.076 0.011 7.263 0.000
#> y4 (bx) 0.024 0.011 2.168 0.030
#> x6 ~
#> x5 (ax) 0.076 0.011 7.263 0.000
#> y5 (bx) 0.024 0.011 2.168 0.030
#> x7 ~
#> x6 (ax) 0.076 0.011 7.263 0.000
#> y6 (bx) 0.024 0.011 2.168 0.030
#> x8 ~
#> x7 (ax) 0.076 0.011 7.263 0.000
#> y7 (bx) 0.024 0.011 2.168 0.030
#> x9 ~
#> x8 (ax) 0.076 0.011 7.263 0.000
#> y8 (bx) 0.024 0.011 2.168 0.030
#> x10 ~
#> x9 (ax) 0.076 0.011 7.263 0.000
#> y9 (bx) 0.024 0.011 2.168 0.030
#> x11 ~
#> x10 (ax) 0.076 0.011 7.263 0.000
#> y10 (bx) 0.024 0.011 2.168 0.030
#> y2 ~
#> x1 (by) 0.027 0.009 2.926 0.003
#> y1 (ay) 0.072 0.011 6.631 0.000
#> y3 ~
#> x2 (by) 0.027 0.009 2.926 0.003
#> y2 (ay) 0.072 0.011 6.631 0.000
#> y4 ~
#> x3 (by) 0.027 0.009 2.926 0.003
#> y3 (ay) 0.072 0.011 6.631 0.000
#> y5 ~
#> x4 (by) 0.027 0.009 2.926 0.003
#> y4 (ay) 0.072 0.011 6.631 0.000
#> y6 ~
#> x5 (by) 0.027 0.009 2.926 0.003
#> y5 (ay) 0.072 0.011 6.631 0.000
#> y7 ~
#> x6 (by) 0.027 0.009 2.926 0.003
#> y6 (ay) 0.072 0.011 6.631 0.000
#> y8 ~
#> x7 (by) 0.027 0.009 2.926 0.003
#> y7 (ay) 0.072 0.011 6.631 0.000
#> y9 ~
#> x8 (by) 0.027 0.009 2.926 0.003
#> y8 (ay) 0.072 0.011 6.631 0.000
#> y10 ~
#> x9 (by) 0.027 0.009 2.926 0.003
#> y9 (ay) 0.072 0.011 6.631 0.000
#> y11 ~
#> x10 (by) 0.027 0.009 2.926 0.003
#> y10 (ay) 0.072 0.011 6.631 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.114 0.023 5.062 0.000
#> wx2 ~~
#> wy2 0.052 0.019 2.801 0.005
#> wx3 ~~
#> wy3 0.092 0.018 5.091 0.000
#> wx4 ~~
#> wy4 0.100 0.018 5.440 0.000
#> wx5 ~~
#> wy5 0.081 0.021 3.936 0.000
#> wx6 ~~
#> wy6 0.061 0.016 3.837 0.000
#> wx7 ~~
#> wy7 0.079 0.015 5.258 0.000
#> wx8 ~~
#> wy8 0.064 0.017 3.698 0.000
#> wx9 ~~
#> wy9 0.068 0.018 3.746 0.000
#> wx10 ~~
#> wy10 0.036 0.020 1.799 0.072
#> wx11 ~~
#> wy11 0.119 0.023 5.245 0.000
#> .RIx ~~
#> .RIy 0.282 0.025 11.367 0.000
#> .RIsx ~~
#> .RIsy 0.002 0.000 4.159 0.000
#> .RIx ~~
#> .RIsx -0.022 0.004 -5.929 0.000
#> .RIy ~~
#> .RIsy -0.013 0.003 -4.447 0.000
#> .RIx ~~
#> .RIsy -0.003 0.003 -1.121 0.262
#> .RIy ~~
#> .RIsx -0.003 0.003 -1.109 0.267
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.746 0.039 19.316 0.000
#> .RIy 0.482 0.029 16.560 0.000
#> .RIsx 0.005 0.001 9.142 0.000
#> .RIsy 0.003 0.000 6.925 0.000
#> wx1 0.634 0.031 20.236 0.000
#> wy1 0.584 0.028 20.528 0.000
#> wx2 0.591 0.027 21.858 0.000
#> wy2 0.495 0.023 21.300 0.000
#> wx3 0.546 0.024 22.466 0.000
#> wy3 0.485 0.022 21.877 0.000
#> wx4 0.572 0.026 22.085 0.000
#> wy4 0.466 0.022 21.369 0.000
#> wx5 0.697 0.029 23.839 0.000
#> wy5 0.543 0.023 23.169 0.000
#> wx6 0.492 0.022 22.859 0.000
#> wy6 0.407 0.019 21.982 0.000
#> wx7 0.448 0.020 22.275 0.000
#> wy7 0.423 0.019 22.154 0.000
#> wx8 0.498 0.022 22.311 0.000
#> wy8 0.472 0.021 22.196 0.000
#> wx9 0.531 0.025 21.539 0.000
#> wy9 0.453 0.022 20.814 0.000
#> wx10 0.490 0.025 19.383 0.000
#> wy10 0.467 0.024 19.368 0.000
#> wx11 0.570 0.030 18.710 0.000
#> wy11 0.503 0.028 18.049 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.004 0.015 0.270 0.787
#> dif2 -0.004 0.014 -0.267 0.789
#> dif3 0.003 0.002 1.494 0.135
#> dif4 -0.001 0.000 -1.904 0.057
#>
#> lavaan 0.6-11 ended normally after 103 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1230
#>
#> Model Test User Model:
#>
#> Test statistic 671.759
#> Degrees of freedom 268
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.094 0.002 60.054 0.000
#> RIy ~
#> oply (ey) 0.104 0.002 65.067 0.000
#> RIsx ~
#> oplx (fx) -0.000 0.000 -1.214 0.225
#> RIsy ~
#> oply (fy) -0.000 0.000 -0.749 0.454
#> x2 ~
#> x1 (ax) 0.045 0.010 4.475 0.000
#> y1 (bx) 0.030 0.010 3.179 0.001
#> x3 ~
#> x2 (ax) 0.045 0.010 4.475 0.000
#> y2 (bx) 0.030 0.010 3.179 0.001
#> x4 ~
#> x3 (ax) 0.045 0.010 4.475 0.000
#> y3 (bx) 0.030 0.010 3.179 0.001
#> x5 ~
#> x4 (ax) 0.045 0.010 4.475 0.000
#> y4 (bx) 0.030 0.010 3.179 0.001
#> x6 ~
#> x5 (ax) 0.045 0.010 4.475 0.000
#> y5 (bx) 0.030 0.010 3.179 0.001
#> x7 ~
#> x6 (ax) 0.045 0.010 4.475 0.000
#> y6 (bx) 0.030 0.010 3.179 0.001
#> x8 ~
#> x7 (ax) 0.045 0.010 4.475 0.000
#> y7 (bx) 0.030 0.010 3.179 0.001
#> x9 ~
#> x8 (ax) 0.045 0.010 4.475 0.000
#> y8 (bx) 0.030 0.010 3.179 0.001
#> x10 ~
#> x9 (ax) 0.045 0.010 4.475 0.000
#> y9 (bx) 0.030 0.010 3.179 0.001
#> x11 ~
#> x10 (ax) 0.045 0.010 4.475 0.000
#> y10 (bx) 0.030 0.010 3.179 0.001
#> y2 ~
#> x1 (by) 0.016 0.009 1.735 0.083
#> y1 (ay) 0.045 0.010 4.525 0.000
#> y3 ~
#> x2 (by) 0.016 0.009 1.735 0.083
#> y2 (ay) 0.045 0.010 4.525 0.000
#> y4 ~
#> x3 (by) 0.016 0.009 1.735 0.083
#> y3 (ay) 0.045 0.010 4.525 0.000
#> y5 ~
#> x4 (by) 0.016 0.009 1.735 0.083
#> y4 (ay) 0.045 0.010 4.525 0.000
#> y6 ~
#> x5 (by) 0.016 0.009 1.735 0.083
#> y5 (ay) 0.045 0.010 4.525 0.000
#> y7 ~
#> x6 (by) 0.016 0.009 1.735 0.083
#> y6 (ay) 0.045 0.010 4.525 0.000
#> y8 ~
#> x7 (by) 0.016 0.009 1.735 0.083
#> y7 (ay) 0.045 0.010 4.525 0.000
#> y9 ~
#> x8 (by) 0.016 0.009 1.735 0.083
#> y8 (ay) 0.045 0.010 4.525 0.000
#> y10 ~
#> x9 (by) 0.016 0.009 1.735 0.083
#> y9 (ay) 0.045 0.010 4.525 0.000
#> y11 ~
#> x10 (by) 0.016 0.009 1.735 0.083
#> y10 (ay) 0.045 0.010 4.525 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.039 0.013 3.029 0.002
#> wx2 ~~
#> wy2 0.041 0.013 3.218 0.001
#> wx3 ~~
#> wy3 0.020 0.011 1.816 0.069
#> wx4 ~~
#> wy4 0.038 0.011 3.536 0.000
#> wx5 ~~
#> wy5 0.040 0.011 3.770 0.000
#> wx6 ~~
#> wy6 0.024 0.011 2.267 0.023
#> wx7 ~~
#> wy7 0.032 0.011 2.846 0.004
#> wx8 ~~
#> wy8 0.026 0.011 2.409 0.016
#> wx9 ~~
#> wy9 0.010 0.013 0.829 0.407
#> wx10 ~~
#> wy10 0.041 0.013 3.203 0.001
#> wx11 ~~
#> wy11 0.054 0.013 4.179 0.000
#> .RIx ~~
#> .RIy 0.345 0.020 17.055 0.000
#> .RIsx ~~
#> .RIsy 0.001 0.000 3.214 0.001
#> .RIx ~~
#> .RIsx -0.013 0.002 -5.989 0.000
#> .RIy ~~
#> .RIsy -0.016 0.002 -7.090 0.000
#> .RIx ~~
#> .RIsy -0.010 0.002 -5.070 0.000
#> .RIy ~~
#> .RIsx -0.007 0.002 -3.652 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 0.579 0.027 21.592 0.000
#> .RIy 0.577 0.026 21.949 0.000
#> .RIsx 0.001 0.000 5.600 0.000
#> .RIsy 0.002 0.000 6.184 0.000
#> wx1 0.416 0.019 21.689 0.000
#> wy1 0.339 0.017 20.520 0.000
#> wx2 0.383 0.017 22.667 0.000
#> wy2 0.404 0.017 23.284 0.000
#> wx3 0.332 0.015 22.866 0.000
#> wy3 0.298 0.013 22.324 0.000
#> wx4 0.312 0.014 22.295 0.000
#> wy4 0.313 0.014 22.208 0.000
#> wx5 0.322 0.014 23.460 0.000
#> wy5 0.328 0.014 23.418 0.000
#> wx6 0.347 0.015 23.609 0.000
#> wy6 0.301 0.013 23.213 0.000
#> wx7 0.347 0.015 23.416 0.000
#> wy7 0.324 0.014 23.455 0.000
#> wx8 0.315 0.014 22.654 0.000
#> wy8 0.320 0.014 22.812 0.000
#> wx9 0.360 0.016 22.425 0.000
#> wy9 0.361 0.016 22.117 0.000
#> wx10 0.348 0.017 20.643 0.000
#> wy10 0.318 0.016 20.315 0.000
#> wx11 0.340 0.017 19.702 0.000
#> wy11 0.300 0.016 18.672 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.000 0.014 0.026 0.980
#> dif2 0.014 0.013 1.153 0.249
#> dif3 -0.009 0.002 -5.209 0.000
#> dif4 -0.000 0.000 -0.337 0.736
#>
#> lavaan 0.6-11 ended normally after 123 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1290
#>
#> Model Test User Model:
#>
#> Test statistic 5437.473
#> Degrees of freedom 268
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.322 0.002 144.287 0.000
#> RIy ~
#> oply (ey) 0.335 0.002 141.169 0.000
#> RIsx ~
#> oplx (fx) 0.000 0.000 2.606 0.009
#> RIsy ~
#> oply (fy) 0.000 0.000 2.659 0.008
#> x2 ~
#> x1 (ax) -0.060 0.008 -7.469 0.000
#> y1 (bx) 0.080 0.008 10.062 0.000
#> x3 ~
#> x2 (ax) -0.060 0.008 -7.469 0.000
#> y2 (bx) 0.080 0.008 10.062 0.000
#> x4 ~
#> x3 (ax) -0.060 0.008 -7.469 0.000
#> y3 (bx) 0.080 0.008 10.062 0.000
#> x5 ~
#> x4 (ax) -0.060 0.008 -7.469 0.000
#> y4 (bx) 0.080 0.008 10.062 0.000
#> x6 ~
#> x5 (ax) -0.060 0.008 -7.469 0.000
#> y5 (bx) 0.080 0.008 10.062 0.000
#> x7 ~
#> x6 (ax) -0.060 0.008 -7.469 0.000
#> y6 (bx) 0.080 0.008 10.062 0.000
#> x8 ~
#> x7 (ax) -0.060 0.008 -7.469 0.000
#> y7 (bx) 0.080 0.008 10.062 0.000
#> x9 ~
#> x8 (ax) -0.060 0.008 -7.469 0.000
#> y8 (bx) 0.080 0.008 10.062 0.000
#> x10 ~
#> x9 (ax) -0.060 0.008 -7.469 0.000
#> y9 (bx) 0.080 0.008 10.062 0.000
#> x11 ~
#> x10 (ax) -0.060 0.008 -7.469 0.000
#> y10 (bx) 0.080 0.008 10.062 0.000
#> y2 ~
#> x1 (by) 0.079 0.008 10.245 0.000
#> y1 (ay) -0.055 0.008 -7.091 0.000
#> y3 ~
#> x2 (by) 0.079 0.008 10.245 0.000
#> y2 (ay) -0.055 0.008 -7.091 0.000
#> y4 ~
#> x3 (by) 0.079 0.008 10.245 0.000
#> y3 (ay) -0.055 0.008 -7.091 0.000
#> y5 ~
#> x4 (by) 0.079 0.008 10.245 0.000
#> y4 (ay) -0.055 0.008 -7.091 0.000
#> y6 ~
#> x5 (by) 0.079 0.008 10.245 0.000
#> y5 (ay) -0.055 0.008 -7.091 0.000
#> y7 ~
#> x6 (by) 0.079 0.008 10.245 0.000
#> y6 (ay) -0.055 0.008 -7.091 0.000
#> y8 ~
#> x7 (by) 0.079 0.008 10.245 0.000
#> y7 (ay) -0.055 0.008 -7.091 0.000
#> y9 ~
#> x8 (by) 0.079 0.008 10.245 0.000
#> y8 (ay) -0.055 0.008 -7.091 0.000
#> y10 ~
#> x9 (by) 0.079 0.008 10.245 0.000
#> y9 (ay) -0.055 0.008 -7.091 0.000
#> y11 ~
#> x10 (by) 0.079 0.008 10.245 0.000
#> y10 (ay) -0.055 0.008 -7.091 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.065 0.010 6.202 0.000
#> wx2 ~~
#> wy2 0.034 0.008 4.100 0.000
#> wx3 ~~
#> wy3 0.065 0.009 7.512 0.000
#> wx4 ~~
#> wy4 0.030 0.008 3.877 0.000
#> wx5 ~~
#> wy5 0.038 0.007 5.206 0.000
#> wx6 ~~
#> wy6 0.037 0.007 5.555 0.000
#> wx7 ~~
#> wy7 0.032 0.007 4.668 0.000
#> wx8 ~~
#> wy8 0.024 0.007 3.368 0.001
#> wx9 ~~
#> wy9 0.033 0.008 4.281 0.000
#> wx10 ~~
#> wy10 0.063 0.010 6.512 0.000
#> wx11 ~~
#> wy11 0.055 0.009 5.930 0.000
#> .RIx ~~
#> .RIy 1.047 0.044 23.905 0.000
#> .RIsx ~~
#> .RIsy 0.000 0.000 1.325 0.185
#> .RIx ~~
#> .RIsx -0.012 0.003 -4.256 0.000
#> .RIy ~~
#> .RIsy -0.017 0.003 -5.846 0.000
#> .RIx ~~
#> .RIsy -0.006 0.003 -2.163 0.031
#> .RIy ~~
#> .RIsx -0.002 0.003 -0.755 0.450
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.665 0.052 31.990 0.000
#> .RIy 1.780 0.055 32.356 0.000
#> .RIsx 0.002 0.000 9.412 0.000
#> .RIsy 0.002 0.000 10.107 0.000
#> wx1 0.281 0.014 19.895 0.000
#> wy1 0.283 0.014 20.425 0.000
#> wx2 0.249 0.012 20.973 0.000
#> wy2 0.205 0.010 20.001 0.000
#> wx3 0.239 0.011 22.202 0.000
#> wy3 0.282 0.012 22.850 0.000
#> wx4 0.206 0.010 21.568 0.000
#> wy4 0.229 0.010 21.933 0.000
#> wx5 0.235 0.010 22.805 0.000
#> wy5 0.186 0.008 22.334 0.000
#> wx6 0.206 0.009 22.323 0.000
#> wy6 0.176 0.008 21.927 0.000
#> wx7 0.200 0.009 22.423 0.000
#> wy7 0.194 0.009 22.241 0.000
#> wx8 0.204 0.009 21.698 0.000
#> wy8 0.208 0.009 22.250 0.000
#> wx9 0.222 0.011 21.147 0.000
#> wy9 0.190 0.009 20.769 0.000
#> wx10 0.243 0.012 20.177 0.000
#> wy10 0.235 0.012 19.995 0.000
#> wx11 0.218 0.012 17.891 0.000
#> wy11 0.197 0.012 17.115 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 -0.005 0.012 -0.381 0.703
#> dif2 0.000 0.012 0.034 0.973
#> dif3 -0.013 0.002 -5.475 0.000
#> dif4 -0.000 0.000 -0.120 0.905
#>
#> lavaan 0.6-11 ended normally after 96 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 87
#> Number of equality constraints 36
#>
#> Number of observations 3283
#> Number of missing patterns 1309
#>
#> Model Test User Model:
#>
#> Test statistic 5808.751
#> Degrees of freedom 268
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> RIx =~
#> x1 1.000
#> x2 1.000
#> x3 1.000
#> x4 1.000
#> x5 1.000
#> x6 1.000
#> x7 1.000
#> x8 1.000
#> x9 1.000
#> x10 1.000
#> x11 1.000
#> RIy =~
#> y1 1.000
#> y2 1.000
#> y3 1.000
#> y4 1.000
#> y5 1.000
#> y6 1.000
#> y7 1.000
#> y8 1.000
#> y9 1.000
#> y10 1.000
#> y11 1.000
#> RIsx =~
#> x1 1.000
#> x2 2.000
#> x3 3.000
#> x4 4.000
#> x5 5.000
#> x6 6.000
#> x7 7.000
#> x8 8.000
#> x9 9.000
#> x10 10.000
#> x11 11.000
#> RIsy =~
#> y1 1.000
#> y2 2.000
#> y3 3.000
#> y4 4.000
#> y5 5.000
#> y6 6.000
#> y7 7.000
#> y8 8.000
#> y9 9.000
#> y10 10.000
#> y11 11.000
#> wx1 =~
#> x1 1.000
#> wx2 =~
#> x2 1.000
#> wx3 =~
#> x3 1.000
#> wx4 =~
#> x4 1.000
#> wx5 =~
#> x5 1.000
#> wx6 =~
#> x6 1.000
#> wx7 =~
#> x7 1.000
#> wx8 =~
#> x8 1.000
#> wx9 =~
#> x9 1.000
#> wx10 =~
#> x10 1.000
#> wx11 =~
#> x11 1.000
#> wy1 =~
#> y1 1.000
#> wy2 =~
#> y2 1.000
#> wy3 =~
#> y3 1.000
#> wy4 =~
#> y4 1.000
#> wy5 =~
#> y5 1.000
#> wy6 =~
#> y6 1.000
#> wy7 =~
#> y7 1.000
#> wy8 =~
#> y8 1.000
#> wy9 =~
#> y9 1.000
#> wy10 =~
#> y10 1.000
#> wy11 =~
#> y11 1.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> RIx ~
#> oplx (ex) 0.263 0.002 110.425 0.000
#> RIy ~
#> oply (ey) 0.290 0.002 122.043 0.000
#> RIsx ~
#> oplx (fx) 0.001 0.000 4.283 0.000
#> RIsy ~
#> oply (fy) -0.001 0.000 -2.612 0.009
#> x2 ~
#> x1 (ax) -0.024 0.008 -2.870 0.004
#> y1 (bx) 0.059 0.008 7.391 0.000
#> x3 ~
#> x2 (ax) -0.024 0.008 -2.870 0.004
#> y2 (bx) 0.059 0.008 7.391 0.000
#> x4 ~
#> x3 (ax) -0.024 0.008 -2.870 0.004
#> y3 (bx) 0.059 0.008 7.391 0.000
#> x5 ~
#> x4 (ax) -0.024 0.008 -2.870 0.004
#> y4 (bx) 0.059 0.008 7.391 0.000
#> x6 ~
#> x5 (ax) -0.024 0.008 -2.870 0.004
#> y5 (bx) 0.059 0.008 7.391 0.000
#> x7 ~
#> x6 (ax) -0.024 0.008 -2.870 0.004
#> y6 (bx) 0.059 0.008 7.391 0.000
#> x8 ~
#> x7 (ax) -0.024 0.008 -2.870 0.004
#> y7 (bx) 0.059 0.008 7.391 0.000
#> x9 ~
#> x8 (ax) -0.024 0.008 -2.870 0.004
#> y8 (bx) 0.059 0.008 7.391 0.000
#> x10 ~
#> x9 (ax) -0.024 0.008 -2.870 0.004
#> y9 (bx) 0.059 0.008 7.391 0.000
#> x11 ~
#> x10 (ax) -0.024 0.008 -2.870 0.004
#> y10 (bx) 0.059 0.008 7.391 0.000
#> y2 ~
#> x1 (by) 0.081 0.008 9.788 0.000
#> y1 (ay) -0.034 0.008 -4.213 0.000
#> y3 ~
#> x2 (by) 0.081 0.008 9.788 0.000
#> y2 (ay) -0.034 0.008 -4.213 0.000
#> y4 ~
#> x3 (by) 0.081 0.008 9.788 0.000
#> y3 (ay) -0.034 0.008 -4.213 0.000
#> y5 ~
#> x4 (by) 0.081 0.008 9.788 0.000
#> y4 (ay) -0.034 0.008 -4.213 0.000
#> y6 ~
#> x5 (by) 0.081 0.008 9.788 0.000
#> y5 (ay) -0.034 0.008 -4.213 0.000
#> y7 ~
#> x6 (by) 0.081 0.008 9.788 0.000
#> y6 (ay) -0.034 0.008 -4.213 0.000
#> y8 ~
#> x7 (by) 0.081 0.008 9.788 0.000
#> y7 (ay) -0.034 0.008 -4.213 0.000
#> y9 ~
#> x8 (by) 0.081 0.008 9.788 0.000
#> y8 (ay) -0.034 0.008 -4.213 0.000
#> y10 ~
#> x9 (by) 0.081 0.008 9.788 0.000
#> y9 (ay) -0.034 0.008 -4.213 0.000
#> y11 ~
#> x10 (by) 0.081 0.008 9.788 0.000
#> y10 (ay) -0.034 0.008 -4.213 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> wx1 ~~
#> wy1 0.131 0.016 8.063 0.000
#> wx2 ~~
#> wy2 0.052 0.013 4.095 0.000
#> wx3 ~~
#> wy3 0.061 0.013 4.836 0.000
#> wx4 ~~
#> wy4 0.035 0.012 2.899 0.004
#> wx5 ~~
#> wy5 0.019 0.012 1.592 0.111
#> wx6 ~~
#> wy6 0.060 0.012 5.030 0.000
#> wx7 ~~
#> wy7 0.051 0.011 4.469 0.000
#> wx8 ~~
#> wy8 0.046 0.012 3.816 0.000
#> wx9 ~~
#> wy9 0.041 0.013 3.183 0.001
#> wx10 ~~
#> wy10 0.052 0.014 3.843 0.000
#> wx11 ~~
#> wy11 0.054 0.016 3.406 0.001
#> .RIx ~~
#> .RIy 0.966 0.044 21.726 0.000
#> .RIsx ~~
#> .RIsy -0.000 0.000 -1.221 0.222
#> .RIx ~~
#> .RIsx -0.026 0.004 -7.036 0.000
#> .RIy ~~
#> .RIsy -0.026 0.004 -7.098 0.000
#> .RIx ~~
#> .RIsy -0.006 0.003 -1.819 0.069
#> .RIy ~~
#> .RIsx -0.002 0.003 -0.509 0.611
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#> .RIx 0.000
#> .RIy 0.000
#> .RIsx 0.000
#> .RIsy 0.000
#> wx1 0.000
#> wx2 0.000
#> wx3 0.000
#> wx4 0.000
#> wx5 0.000
#> wx6 0.000
#> wx7 0.000
#> wx8 0.000
#> wx9 0.000
#> wx10 0.000
#> wx11 0.000
#> wy1 0.000
#> wy2 0.000
#> wy3 0.000
#> wy4 0.000
#> wy5 0.000
#> wy6 0.000
#> wy7 0.000
#> wy8 0.000
#> wy9 0.000
#> wy10 0.000
#> wy11 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .RIx 1.724 0.058 29.671 0.000
#> .RIy 1.534 0.053 28.805 0.000
#> .RIsx 0.003 0.000 9.076 0.000
#> .RIsy 0.003 0.000 9.228 0.000
#> wx1 0.443 0.022 20.212 0.000
#> wy1 0.422 0.021 20.054 0.000
#> wx2 0.356 0.017 21.061 0.000
#> wy2 0.355 0.017 21.063 0.000
#> wx3 0.365 0.016 22.428 0.000
#> wy3 0.386 0.017 22.367 0.000
#> wx4 0.348 0.016 21.685 0.000
#> wy4 0.311 0.015 21.201 0.000
#> wx5 0.339 0.015 22.638 0.000
#> wy5 0.345 0.015 22.758 0.000
#> wx6 0.360 0.016 23.032 0.000
#> wy6 0.348 0.015 22.762 0.000
#> wx7 0.365 0.016 22.850 0.000
#> wy7 0.301 0.014 22.120 0.000
#> wx8 0.333 0.015 22.202 0.000
#> wy8 0.366 0.016 22.401 0.000
#> wx9 0.356 0.017 21.419 0.000
#> wy9 0.357 0.017 21.258 0.000
#> wx10 0.322 0.017 19.326 0.000
#> wy10 0.345 0.018 19.361 0.000
#> wx11 0.401 0.021 19.206 0.000
#> wy11 0.337 0.019 17.681 0.000
#> .x1 0.000
#> .x2 0.000
#> .x3 0.000
#> .x4 0.000
#> .x5 0.000
#> .x6 0.000
#> .x7 0.000
#> .x8 0.000
#> .x9 0.000
#> .x10 0.000
#> .x11 0.000
#> .y1 0.000
#> .y2 0.000
#> .y3 0.000
#> .y4 0.000
#> .y5 0.000
#> .y6 0.000
#> .y7 0.000
#> .y8 0.000
#> .y9 0.000
#> .y10 0.000
#> .y11 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> dif1 0.010 0.012 0.816 0.415
#> dif2 -0.022 0.012 -1.787 0.074
#> dif3 -0.027 0.002 -10.782 0.000
#> dif4 0.001 0.000 5.018 0.0003.6.8 Summary results hypo2
| paths | est | se | pvalue | est | se | pvalue | est | se | pvalue | est | se | pvalue |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| eu-integration | ||||||||||||
| Men:stability | 0.60 | 0.01 | 0 | 0.13 | 0.01 | 0.00 | 0.22 | 0.01 | 0 | 0.08 | 0.01 | 0.00 |
| Women:stability | 0.52 | 0.01 | 0 | 0.10 | 0.01 | 0.00 | 0.19 | 0.01 | 0 | 0.07 | 0.01 | 0.00 |
| Men:partner-effect | 0.16 | 0.01 | 0 | 0.00 | 0.01 | 0.67 | 0.06 | 0.01 | 0 | 0.02 | 0.01 | 0.03 |
| Women:partner-effect | 0.15 | 0.01 | 0 | 0.03 | 0.01 | 0.00 | 0.08 | 0.01 | 0 | 0.03 | 0.01 | 0.00 |
| immigrants | ||||||||||||
| Men:stability | 0.57 | 0.01 | 0 | 0.06 | 0.01 | 0.00 | 0.10 | 0.01 | 0 | 0.05 | 0.01 | 0.00 |
| Women:stability | 0.57 | 0.01 | 0 | 0.06 | 0.01 | 0.00 | 0.10 | 0.01 | 0 | 0.04 | 0.01 | 0.00 |
| Men:partner-effect | 0.18 | 0.01 | 0 | 0.03 | 0.01 | 0.00 | 0.05 | 0.01 | 0 | 0.03 | 0.01 | 0.00 |
| Women:partner-effect | 0.15 | 0.01 | 0 | 0.01 | 0.01 | 0.26 | 0.04 | 0.01 | 0 | 0.02 | 0.01 | 0.08 |
| euthanasia | ||||||||||||
| Men:stability | 0.66 | 0.01 | 0 | -0.03 | 0.01 | 0.00 | 0.15 | 0.01 | 0 | -0.06 | 0.01 | 0.00 |
| Women:stability | 0.70 | 0.01 | 0 | -0.02 | 0.01 | 0.00 | 0.14 | 0.01 | 0 | -0.06 | 0.01 | 0.00 |
| Men:partner-effect | 0.19 | 0.01 | 0 | 0.06 | 0.01 | 0.00 | 0.17 | 0.01 | 0 | 0.08 | 0.01 | 0.00 |
| Women:partner-effect | 0.17 | 0.01 | 0 | 0.06 | 0.01 | 0.00 | 0.16 | 0.01 | 0 | 0.08 | 0.01 | 0.00 |
| income_diff | ||||||||||||
| Men:stability | 0.61 | 0.01 | 0 | 0.02 | 0.01 | 0.04 | 0.16 | 0.01 | 0 | -0.02 | 0.01 | 0.00 |
| Women:stability | 0.54 | 0.01 | 0 | 0.00 | 0.01 | 0.69 | 0.12 | 0.01 | 0 | -0.03 | 0.01 | 0.00 |
| Men:partner-effect | 0.14 | 0.01 | 0 | 0.04 | 0.01 | 0.00 | 0.14 | 0.01 | 0 | 0.06 | 0.01 | 0.00 |
| Women:partner-effect | 0.15 | 0.01 | 0 | 0.05 | 0.01 | 0.00 | 0.13 | 0.01 | 0 | 0.08 | 0.01 | 0.00 |
3.7 Assignment
- Look in the literature for other measures of opinion homophily. Try to apply this measure to construct a similar table as 3.5.
- Have a look at the detailed results of the RI-CLPM estimated for hypothesis 1. Could you conclude, based on the error-covariance and/or error-correlation between the opinions of the spouses that opinion homophily increased? Motivate your answer.
- Have a look at the detailed results of the LT-RI-CLPM and focus on the variance and covariance of the random slopes of the partners. What does this tell you about opinion homophily within partners? Motivate your answer.
- You see that sections 3.6.6 and 3.6.9 are empty. Please fill in the blanks. Motivate your answer and discuss both selection and influence.
- You could argue that influence is only possible if people differ initially. Please select couples who are dissimilar at within-time 1 and do the descriptive and analysis part again. Of course, of course, not for all dependent variables and modelling specifications. Pick one dependent and focus on the RI-CLPM.
- Please test if influence processes depend on educational attainment. Thus, formulate a hypothesis and test this hypothesis.
References
I am assuming that spouses - and egos/alters more generally - can be ‘distinguished’. If this is not the case (e.g. homosexual couples), we need different techniques.↩︎
Except of course if you face issues of multicollinearity.↩︎
One of the reasons couples drop out of our data is because of divorce.↩︎
